UNA DEMOSTRACIÓN GRÁFICA DE LA CUADRATURA DEL CIRCULO (dejando de lado la regla y el compás)

La cuadratura del círculo fue uno de los conocidos como tres problemas clásicos griegos. Los otros dos problemas eran la trisección del ángulo y duplicación del cubo, pero cuando decimos cuadratura del círculo parece que nos referimos a algo absurdo, a la existencia de un circulo con esquinas, pero debemos recordar que, en terminología matemática   cuadratura significa otra cosa. El diccionario de la RAE recoge el significado que se utiliza en Geometría en su cuarta acepción, a continuación, recogemos las cuatro primeras acepciones de la palabra cuadrar, que significa:

1. 1. 1. Dar a algo forma de cuadrado.
      2. Hacer que coincidan los totales del debe y del haber de una cuenta, un balance, etc.
      3. (Carpintería). Trabajar o formar los maderos en cuadro.
      4. (Geom.) Determinar el cuadrado equivalente en superficie a una figura dada.

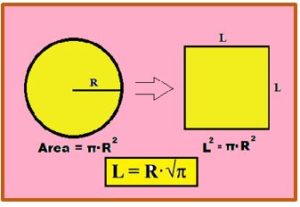
Luego el problema de la cuadratura del círculo sería construir un cuadrado que tuviera la misma área que un circulo dado (tal y como se recoge en la imagen anterior). El problema en si es complicado, pero los griegos aún le impusieron la condición adicional que fue que la construcción se hiciera usando únicamente la regla y el compás y esta exigencia lo convirtió en un problema irresoluble.

Pero, como sucede hasta cuando se trata de solucionar un problema irresoluble bajo ciertas condiciones, se realizaron muchos intentos, que abrieron varias líneas de trabajo para abordarlo.

El primer método fue el seguido al más puro estilo de la geometría euclidiana, por matemáticos, como Hipócrates de Quios (470 y el 410 a. de C.), que conocían el método de cuadrar polígonos de cualquier número de lados y también cuadrar algunas figuras con perímetro curvo, como las lúnulas, y confiaban en encontrar un método análogo para el círculo.

El segundo método estaba orientado a hallar la relación numérica entre la circunferencia y  el diámetro de la misma que sería un valor fijo para  todos los círculos, p, una el área sería la de un rectángulo de base pr y de altura r, pero quedaba una indeterminación en la rectificación dela circunferencia, es por lo que  Aristóteles en su Física calificó de grosero el método de Antifonte de Atenas (480-411 a. de C.), que parece que era el sofista que lo mantenía, por lo que el procedimiento fue tenido en poca consideración por los filósofos posteriores. No obstante, Arquímedes hizo el cálculo de π aproximando el área del circulo por polígonos de 3·2ⁿ lados inscritos y circunscritos obteniendo una acotación.

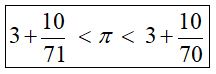
El tercer método consistió en utilizar curvas mecánicas, no definidas dentro de la geometría euclidiana y que tomaban el valor de  π para una abscisa dada. Esta línea fue la línea seguida por  Hipias de Élide (443- 399 a.de C.)​ y  Dinóstrato ( 390-320 a. de C ), que utilizó la trisectriz de Hipias para resolver (sin el uso de la regla y el compás) el problema de la cuadratura del círculo.  

La curva  de Hipias, se genera por el movimiento así: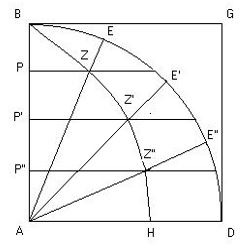

1. BG se desplaza en paralelo con movimiento uniforme hasta AD
2. AB gira con centro A y movimiento uniforme hasta AD
3. BG y AB inician a la vez sus movimientos
4. BG y AB llegan a la vez a AD
5. La curva cuadratriz se genera por los puntos de intersección de BG y AB Z, Z’,Z’’…

Como BG se desplaza paralelamente con movimiento uniforme, AB gira con movimiento uniforme con centro B y los dos segmentos alcanzan en punto D al mismo tiempo:

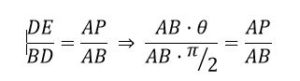
Haciendo AB = 1 y pasando a coordenadas polares:

Tomando limites, cuando  θ tiende a  0, entonces  x tiende a AH, es decir:

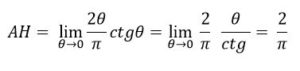
ya que la curva permite determinar (geométricamente) el valor de pi.

Pero esta demostración no era válida en geometría, ya que no estaban definidos los movimientos. En la geometría euclidiana los movimientos físicos, como el que se han expuesto en esta demostración estaba sustituido por el de figuras congruentes (dos figuras u objetos son congruentes si tienen el mismo tamaño y forma. En el Libro I de los elementos aparecen cuarenta y ocho proposiciones, cada una de ellas están rigurosamente demostradas a partir de las definiciones, de los postulados y de las nociones comunes. De la 1 a la 26, tratan principalmente de las propiedades de los triángulos e incluyen tres proposiciones (24, 24 y 26) sobre congruencia de triángulos bien conocidos.

Si aceptamos el movimiento de rotación aparece una sugerente solución recogida en Demostraciones sin palabras de Roger B Nelsen:

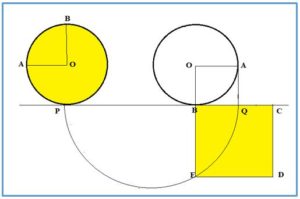
Sea un circulo de radio OB =  r . Que parte de una situación en la que B está en la parte superior

1. 1. 1. 1. El circulo rueda sobre la horizontal PBQC Hasta que B está en la parte inferior
         2. La longitud PB es media circunferencia PB = pi·r y BQ = r
         3. Trazamos una semicircunferencia de diámetro PB BQ = PQ = pi·r + r
         4. El segmento BE es media proporcional entre PB y BQ, lo que significa que:
         5. BE² = PB· BQ , es decir   BE² =  (pi·r) · r = pi·r².
         6. Luego BE es el lado del cuadrado con área igual al círculo.