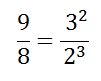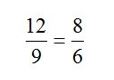Pitágoras (570- 475 a. C) y su Escuela mantenían que el Universo estaba gobernado por leyes matemáticas y que el número formaba parte de la esencia de las cosas. Esta idea era contraria a la que, dos siglos después, defendería Aristóteles (384-322), el cual, aunque apreciaba la belleza de la Geometría del Triángulo y de las matemáticas en general, rechazaba la idea de que los números y los entes geométricos pudieran formar parte la intimidad de la Naturaleza y de los seres.
Los filósofos presocráticos estaban preocupados por comprender la Naturaleza (fisis) y buscaban el principio de las cosas (arjé). Para Thales el principio de todo era el agua, para Anaxímenes el aire, para Heráclito el orden y la armonía del universo procedían de la lucha de contrarios, para Anaximandro todo surgía del ápeiron (lo que no tiene límite, lo indefinido). Esta etapa se considera, dentro de la filosofía griega, como el periodo cosmológico. Aristóteles explicaba que los principios de los filósofos presocráticos se basaban en descubrimientos empíricos y esto sucede con Pitágoras.
Pitágoras se apoyaba en que los intervalos musicales que había entre las notas armónicas de la lira podían expresarse numéricamente. Pero, además, los pitagóricos concibieron los números con representación geométrica (en triángulos, cuadrados, cubos o pirámides), y llegaron a identificar el punto geométrico con la unidad aritmética con lo cual, las unidades aritméticas tenían extensión espacial y podían ser consideradas como los elementos materiales de las cosas. Aceptada esta idea las cosas se podían considerar como agregados de puntos materiales y como conjuntos de unidades numéricas.
Las investigaciones de Pitágoras en acústica le hicieron concebir la idea de que todo lo que existe en la Naturaleza, hasta lo más abstracto, estaba sometido a las leyes de los números. Con la Escuela Pitagórica comenzó estudio de la música como ciencia cuantitativa y de la medida. El propio Pitágoras descubrió una serie de relaciones aritmético-musicales que constituyeron el inicio de la ciencia musical y, seguramente, el primer ejemplo histórico de experimentación científica.
La leyenda transmitida por el pitagórico Jámblico (245-325), cuenta que, al pasar Pitágoras por una herrería, le atrajeron los sonidos que emitían los martillazos que daban cuatro esclavos que trabajaban un trozo de metal al golpear sobre el yunque. Tres de ellos producían sonidos consonantes, mientras que el cuarto producía una disonancia.
Creyendo el sabio que el sonido dependía de la fuerza con que golpeaba el yunque cada uno de los herreros, pidió que se intercambiaran los martillos, pero el resultado fue que el mismo martillo seguía produciendo el sonido disonante cualquiera que fuera el herrero que lo usara. Pitágoras concluyó que la sonoridad no dependía de la fuerza de los esclavos, sino de las características de cada martillo. Al llegar a su casa, realizó la primera experiencia de laboratorio que registra la historia, pesó los martillos, ató sus pesos a cuerdas de igual longitud hasta que emitieran las mismas notas que daban los martillos, entonces descubrió que los tres consonantes tenían pesos proporcionales a 6, 8 y 12 Agregó después, para modificar el peso del cuarto martillo que producía desarmonía, de un trozo de arcilla hasta obtener un sonido agradable, una vez añadida la arcilla, dedujo la relación siguiente:
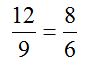
que, según Jámblico, se llama musical porque contiene las relaciones musicales de los sonidos armónicos. De ahí salen las razones (1/2 (octava), 3/4(cuarta) y 2/3 (quinta))
Se ha dicho muchas veces que Pitágoras no pudo realizar el experimento como lo describe Jámblico, ya que, si realmente lo hubiera realizado, habría comprobado que las notas emitidas no guardaban esa relación con los pesos que se colgaban de las cuerdas, sino con la raíz cuadrada de los mismos.
Realmente la relación entre la longitud de la cuerda, su tensión y la frecuencia de la nota emitida por la cuerda al vibrar es
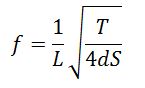
dinde f es la frecuencia, L la longitud de la cuerda, T la tensión, S la sección y d la densidad.
No obstante Pitágoras dio relaciones numéricas entre longitudes de cuerdas sometidas a tensiones iguales y la nota emitida al vibrar. Para ello construyó un instrumento musical llamado monocordio, que constaba de una cuerda sonora, una caja de resonancia y una regla graduada o canon con la que se podía determinar las relaciones numéricas de los diferentes segmentos de la cuerda que sonaba y la nota emitida.
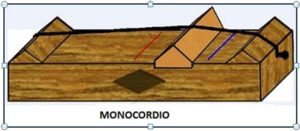
Pitágoras dejó sentadas relaciones musicales como las siguientes. Si se dispone de una cuerda de longitud L a la que mantenemos con una tensión constante y al hacerla vibrar emite una nota C, cuando hacemos vibrar su mitad emite la misma nota C (2/1), que es la octava más aguda. Dividiendo la cuerda en tres partes y haciendo sonar dos se emite la quinta (3/2) de C. Dividiendo en cuatro partes y haciendo sonar tres de ellas se obtiene la cuarta (4/3) de C. Estas notas, al hacerlas sonar conjuntamente o seguidas resultaban agradables, (consonantes) al oído.
El descubrimiento de estas relaciones numéricas entre las notas musicales consonantes lo llevó a pensar que, del mismo modo que había unas relaciones numéricas que regían la armonía musical, debían existir otras relaciones numéricas análogas que gobernaran el universo armonioso en el que se majestuosamente los astros en eternos movimientos circulares. El Universo, con relaciones numéricas análogas a las relaciones musicales, sería semejante a un gran diapasón o caja de música.
Los Pitagóricos atribuyeron a los intervalos planetarios propiedades análogas a los intervalos musicales y concluyeron que el universo, debía emitir una música, quizás no audible, pero tan armoniosa como la música sonora, a la que denominaron música de las esferas.
Las relaciones de la armonía musical condujeron a Pitágoras y a su Escuela a sobreestimar el alcance del descubrimiento y los llevó formular una hipótesis a priori, que era una extrapolación mística.
Realmente los pitagóricos realizaron pocas aportaciones a la física. El núcleo fundamental de sus contribuciones lo constituyó la geometría, pero aportaron al mundo de la ciencia la idea fundamental de que el mundo físico tenía un funcionamiento que podía ser descrito en lenguaje matemático.
La influencia del pitagorismo, sobre todo a través de Platón, fue decisiva en la construcción de la Ciencia Moderna el siglo XVII. Platón destacaba el papel de las Matemáticas en ese largo camino hacia la Dialéctica, con la cuál la mente podía elevarse hasta el mundo de las ideas sin necesidad de apoyarse en la experiencia sensible que podía engañarnos por las imprecisas percepciones de nuestros sentidos e impedirnos lograr una completa contemplación de lo inteligible.
El Demiurgo de la cosmogonía platónica ordenaba el Mundo y conseguía la armonía natural basándose en los modelos matemáticos. Esta idea fue recogida por los pensadores cristianos y daría lugar a la idea de un Dios Geómetra. Como puede verse en multitud de grabados medievales. Como el que aparece en miniado de la Biblia del siglo XIII que encargó de la reina Blanca de Castilla para su hijo Luís IX de Francia, que se conserva en la Catedral de Toledo
El supuesto pitagórico de que el universo tenía una armonía numérica fue asimilada por Galileo (1564-1642) para formular las primeras leyes de la física y expresar este principio pitagórico-platónico con el siguiente lema: La Naturaleza es un libro escrito en lenguaje matemático.
También el astrónomo J. Kepler (1571-1630), participando de la idea pitagórica, partió de la suposición apriorística de que los sólidos platónicos determinaban el espacio entre las órbitas de los planetas.
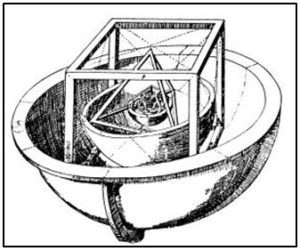
En 1595, Kepler tuvo una idea a la que dio una importancia considerable: ¿por qué el sistema solar tenía seis planetas? ¿Qué relación existía entre los radios de sus órbitas? Kepler asoció esta realidad con el hecho de que Euclides había demostrado que existían cinco poliedros regulares. Cada uno de ellos inscrito en una esfera y circunscrito en otra de mismo centro. Los poliedros podían representar los cinco intervalos que existían entre los seis planetas conocidos. Kepler pensó que esa coincidencia no podía ser fruto del azar, que el Creador actuó como un geómetra y que el hombre era capaz de descubrir el Plan de la Creación y conocer la perfección del mundo creado. Dentro de la órbita o esfera de Saturno Kepler inscribió un cubo; y dentro de éste estaba inscrita la esfera de Júpiter circunscrita a un tetraedro, dentro del cual situó inscrita la esfera de Marte. Finalmente entre las esferas de Marte y la Tierra situó el dodecaedro, entre las esferas la Tierra y Venus el icosaedro, entre las esferas de Venus y Mercurio estaba el octaedro y en el centro de todo el Sistema estaba el Sol.
Cuando en 1602 Kepler pudo acceder a los datos de las observaciones astronómicas del genial T. Brahe (1646-1601) y, como brillante matemático que era, puso a prueba su Sistema del Mundo y no pudo comprender lo que sucedía: su modelo geométrico no se ajustaba a las observaciones Tycho y además, comprobó que los planetas no seguían órbitas circulares, sino elípticas. La racionalidad de la geometría no estaba de acuerdo con la realidad. Sus conclusiones fueron publicadas en el libro Astronomía Nova (1609) donde aparecieron las dos primeras Leyes del movimiento planetario de Kepler. Las dos surgen del análisis y la interpretación matemática de las observaciones astronómicas Brahe: La Primera afirmaba que los planetas se movían alrededor del Sol en órbitas elípticas y el Sol ocupaba uno de sus focos y la Segunda (la Ley de las Áreas) decía que los planetas no se movían con velocidad uniforme, sino de forma que una línea imaginaria trazada del Sol al planeta barría áreas iguales en tiempos iguales.
La Tercera Ley fue descubierta por Kepler más tarde y fue publicada en su libro Harmonia Mundi (1619). En esta obra Kepler vuelve a la visión pitagórica del Universo y a una interpretación particular de la música de las esferas.
Supuso que, durante su movimiento de revolución alrededor del Sol, cada planeta producía un tono musical, cuya la frecuencia variaba con la velocidad angular de los planetas medidas con respecto al Sol. A menor velocidad les correspondería una menor frecuencia del sonido emitido,
El planeta más lejano al Sol, Saturno, era el más lento, por tanto emitiría el sonido más grave, pero, además, por la Ley de las Áreas, en cada planeta cuando la distancia es menor (perihelio) la velocidad tiene que ser mayor y en el afelio menor, lo que significaba que emitían diferentes notas en cada punto de su órbita. De este modo los planetas girarían alrededor del Sol cantando cada uno su melodía orbital y se convertirían en un coro cantando al Astro Rey. En ese coro Mercurio sería la voz soprano, la Tierra y Venus la contralto, Marte el tenor y Saturno y Júpiter las voces de bajo.
Kepler calculó la velocidad de los planetas en los puntos de la órbita en los que se movían más lento y más rápido notando que el movimiento representa a la vibración armónica que la distancia. Finalmente obtuvo que la tercera ley de Kepler que afirma que el cubo del semieje mayor de la órbita (Sol-Afelio) dividida por el cuadrado del período de revolución es el mismo para todos los planetas. Es decir:
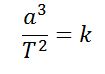ley importante que tuvo en cuenta I. Newton (1642-1927) en el proceso de descubrimiento de la Ley de Gravitación Universal y que tiene una clara analogía con el intervalo entre dos tonos consecutivos en la Escala Musical con afinación pitagórica que era de dos quintas:
