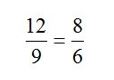Galileo Galilei (1564-1642) en su obra Dialogo sobre los Sistemas del Mundo (1633), calculó la trayectoria de un proyectil lanzado horizontalmente como resultado de la composición dos movimientos simultáneos e independientes entre sí: uno era horizontal y uniforme; otro vertical y uniformemente acelerado y que su trayectoria describía una parábola.
El movimiento en Aristóteles tenía un carácter finalista, era el paso de la potencia al acto y la orientación del mismo estaba perfectamente determinada en cada caso. En lo que se refiere al movimiento local, los cuerpos del mundo sublunar tenían en su naturaleza una especie de motor brújula que los orientaban hacia el centro de la Tierra mientras que los planetas, las estrellas y los demás astros celestes estaban dotados de su movimiento natural propio que era circular. Había otros movimientos forzados o violentos. Los cuerpos con movimientos violentos seguían trayectorias raras, diferentes de rectas y circunferencias. Algunos cuerpos, como las pelotas, que tenían rebotes, o el vuelo de los insectos llevaban trayectorias irregulares. difíciles de determinar.
En este artículo destacaremos un aspecto curioso de la historia de las cónicas. Estas curvas se cuentan entre docena de curvas conocidas en la antigüedad, pasaron más de quince siglos de olvido en los que las cónicas apenas se nombraban y que con la aparición de la ciencia moderna en los siglos XVI y XVII, acabaron convirtiéndose en las curvas estrella.
En el siglo IV a de C, Menecmo (380-320 a.C.), discípulo de Platon y de Eudoxo (390-337) estudió el problema de la duplicación del cubo y lo redujo a la cuestión de intercalar dos medias proporcionales entre 1 y 2 y Aristeo el Viejo (370-300 a.C.) en el Libro de los lugares sólidos, en el que describe a las cónicas por intersección de cilindros y conos con planos). El mismo Euclides (339-275 a. C.), además de los Elementos, escribió un tratado sobre cónicas, aunque no se ha conservado ninguna copia. Pero cualquier obra anterior sobre cónicas quedó eclipsada por el Tratado sobre Cónicas escrito a finales del siglo III a. C, por Apolonio de Perga (262-190 a. C.). Los griegos trabajaron con las cónicas, por ejemplo, Eratóstenes (276-194 a.C.) construyó un instrumento (el mesolabio) para intercalar dos medias proporcionales y resolver así el problema de la duplicación del cubo (aunque no siguiendo la restricción de resolverlo utilizando solamente la regla y el compás).
Las razones fundamentales de la desaparición durante más de quince siglos hay que buscarla en dos hechos. La primera es que, salvo la espiral de Arquímedes, las otras curvas (la cuadratriz de Dinóstrato, la de Hipias, la concoide de Nicomedes o la cisoide de Diocles) se habían pensado para resolver problemas concretos: la cuadratura del círculo, la trisección del ángulo o la duplicación de cubo (y los resolvían, aunque no con regla y compás), mientras que las cónicas y la espiral eran especulaciones matemáticas, curiosidades.
La segunda es que la geometría griega estuvo dominada durante muchos siglos por la geometría de Euclides y en el los Elementos no hay cónicas. El estudio de las mismas no pasaba de ser una cuestión más en la formación geométrica de los filósofos griegos. En todo caso, sería una cuestión especulativa que no tenía correspondencia en el mundo real.
Por otra parte, el estudio de las cónicas no halló lugar en la enseñanza del cuadrivium medieval (aritmética, geometría, astronomía y música), ni se les encontró ninguna aplicación en el estudio de la naturaleza durante más de quince siglos hasta que fueron descubiertas en el movimiento de algunos cuerpos. Los resultados obtenidos por Apolonio se mantuvieron sin cambios hasta que P. Fermat (1607-1665) y P. Descartes (1596-1650), con su aportación genial de la Geometría Analítica que es que una ecuación con dos incógnitas puede considerarse como la determinación de una curva plana.
Con la llegada de la geometría analítica el número de curvas se amplió notablemente. Se podían nombrar y describir por su ecuación infinitas curvas, en concreto, las curvas de la forma y = xn se llamaron parábolas de Fermat (o hipérbolas si n fuera negativo)
Con la geometría analítica, Descartes realizó en su Geometría (1637) un enfoque puramente algebraico de las cónicas y empleó de las ecuaciones de segundo grado para deducir las propiedades de las cónicas y realizar su construcción geométrica. Mientras que Fermat dedujo las ecuaciones de la recta, la circunferencia y las demás secciones cónicas desde la geometría.

B.Mandelbrot (1924-2010) en un artículo publicado en el libro Pensar la Matemática (1984) titulado De Apolonio de Perga a Kepler viene a destacar el olvido con estas palabras:
Los griegos descubrieron las cónicas en estado salvaje en los conos o cilindros y Apolonio las cultivó como un mero juego de ingenio. ¿Cuál sería la sorpresa, cuando quince siglos después, Kepler descubrió que la trayectoria del planeta Marte era elíptica, y Galileo que la caída de las piedras era parabólica
En el siglo XVI J. Kepler (1571-1630) se encontró con la elipse estudiando el movimiento de los planetas, en particular con el estudio de la órbita de Marte, mientras utilizaba las precisas observaciones del astrónomo danés Tycho Brahe (1546-1601).

Kepler se dedicó a poner en orden temporal las observaciones de Tycho y descubrió las que se conocen como tres leyes de Kepler, que cumple el movimiento de los planetas alrededor del Sol. Encontró que las órbitas eran elípticas y no circulares y el Sol ocupaba uno de sus focos. También descubrió que la velocidad de los planetas no era constante, sino que el radio vector que los unía con el Sol barría áreas iguales en tiempos iguales y, en consecuencia, como las órbitas eran elípticas y el Sol estaba en un foco, la velocidad de los planetas era mayor cuando estaban más próximos al Sol (perihelio) que cuando se movían por las zonas más alejadas (afelio). Estos descubrimientos los publicó en su obra Astronomía nova (1609), con ellos, se iniciaba una astronomía que superaba la astronomía observacional del momento, que trataba de salvar las apariencias, y se iniciaba una nueva visión de los cielos que buscaba describir la realidad tal y como era, esto es, comenzaba una astronomía física celeste, que unía la física y la astronomía que anunciaba la llegada de la mecánica celeste.
Años más tarde Galileo encontró la parábola en el mundo físico cuando estudió la velocidad de caída de un cuerpo por un plano inclinado partiendo del reposo. Observó que la velocidad con que llegaba el suelo no dependía de la inclinación del plano sino de la altura o desnivel vertical del que hubiera partido.
Dado que en tiempos de Galileo no había relojes capaces de hacer mediciones de tiempos en movimientos rápidos, esta observación permitía medir la velocidad en de caída libre de un cuerpo calculando la velocidad de caída por un plano inclinado (poco inclinado) por el que tardaba más tiempo en alcanzar la velocidad. Para medir el tiempo utilizó una clepsidra o reloj de agua, que consistía en una vasija llena de agua, que podía verter un hilillo de agua, que medía en una probeta mientras el cuerpo descendía. Luego pesaba el agua recogida en cada descenso, la relación entre los pesos de agua daba la relación entre de los tiempos de descenso.
Midiendo las distancias recorridas por el cuerpo que se deslizaba libremente observó que en el primer intervalo de tiempo recorría una distancia L, en el segundo intervalo 3L, en tercero 5L, en el cuarto 7L, en el enésimo (2n-1) L. Los que indicaba que el movimiento de caída del cuerpo era uniformemente acelerado, ya que la velocidad aumentaba 2L cm/s, es decir, la aceleración era de 2L cm/s2. Por lo tanto, el espacio s recorrido en t segundos era proporcional a t2, ya que:
s = L + 3L + 5L + 7L + ···+ (2t-1) L = [1 + 3 + 5 + 7 + ··· + (2t-1)] L = t2·L = t2·L
Como la aceleración a = 2L cm/s2, podemos escribir:

Por lo tanto, la distancia total recorrida en caída libre en un tiempo t era proporcional a t2. Las distancias recorridas en intervalos sucesivos de tiempo estaban en la proporción 1 : 3 : 5 : 7, etc. Siempre. Cuanto más inclinado fuera el plano, mayores serían las distancias, pero sus relaciones seguían siendo las mismas y esas relaciones se debían cumplir cuando el ángulo fuera α = 90º, esto es, para la caída vertical.
Galileo dedujo que la velocidad del movimiento uniformemente acelerado era proporcional tiempo: vt = a·t.
Debemos observar que en este experimento estudió el movimiento prescindiendo de las causas que lo producen y de la naturaleza del cuerpo en movimiento. Además, a partir de él formuló el principio de inercia, que dice que cualquier cuerpo continuará en estado de reposo o de movimiento rectilíneo a menos que una fuerza externa actúe sobre él. Para Galileo el movimiento y el reposo eran dos estados que un cuerpo podía tener y mantener. El reposo no era un estado especial y un cuerpo se podía encontrar en estado de movimiento o de quieto.
Galileo expuso la nueva visión del movimiento en su libro Demostraciones y consideraciones matemáticas sobre dos nuevas ciencias (1638). Y razonó con planos inclinados para llegar a formular el Principio de Inercia. Observó que la velocidad máxima que alcanzaba un objeto que caía por un plano la alcanzaba en un plano vertical y disminuía a medida que el plano se hacía más horizontal. A partir de la experiencia formuló la siguiente hipótesis: Cuando el plano se acerca a la horizontal, el cuerpo no tiene tendencia a moverse ni ofrecerá resistencia alguna a ser movido, con lo cual concluye que ese movimiento a lo largo de la horizontal puede ser uniforme y perpetuo.
De acuerdo con este principio (Principio de Inercia) de Galileo, el estado natural de los objetos era exclusivamente el reposo (un reposo absoluto), sino también cualquier movimiento rectilíneo y uniforme, ya que, en ausencia de fuerzas, permanece inalterable.

Galileo en Diálogos sobre los dos grandes sistemas del mundo, ptolemaico y copernicano (1632) explicó las leyes del lanzamiento horizontal así:
Sabemos que el movimiento que tendrá lugar sobre un plano será uniforme y perpetuo, en el supuesto de que el plano se prolongue hasta el infinito. Si, por el contrario, el plano es limitado, el móvil que suponemos dotado de gravedad, una vez llegue el extremo del plano y continúe su marcha, añadirá al movimiento precedente, uniforme e inagotable, esta tendencia hacia abajo, debida a la gravedad. Nace así un movimiento descendente naturalmente acelerado. Pues bien, a este tipo de movimiento yo le llamo proyección y hemos de demostrar alguna de sus propiedades, la primera de las cuales es la siguiente
Proposición: Un proyectil que se desplaza con un movimiento compuesto por un movimiento horizontal y uniforme y por un movimiento descendente naturalmente acelerado, describe, en este movimiento, una línea semi-parabólica
Se enfrentaba al problema de calcular la trayectoria de un proyectil, un problema que no había resuelto los artilleros por el enorme lastre que suponía el bagaje a aristotélico que sólo distinguía el movimiento rectilíneo y el circular y que no era posible observar la trayectoria de un proyectil en el aire. Consideró la composición de movimientos
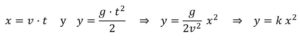
Y se encontró con la parábola que había estudiado, como Kepler, en el olvidado Tratado de Cónicas de Apolonio.
También A.Koiré en Estudios de Historia del Pensamiento Científico (Siglo XXI, Madrid, 1971, cap.4, p.44), se expresa en términos parecidos:
«La meditación sobre los libros de Apolonio hará posible la revolución astronómica operada por Kepler».
Víctor Arenzana Hernández