
Dada una variable aleatoria discreta X que toma los valores x1, x2, x3, …, xn con probabilidades p1, p2, p3, …, pn respectivamente se llama Esperanza Matemática o Valor Esperado de X a la suma de los productos de cada valor de la variable por la probabilidad con la que producen cada uno de los valores de la misma. Es decir:
E(X) = x1·p1 + x2· p2 + x3· p3 … + xn· pn
El nombre de Valor Esperado procede de los juegos de azar. Un juego que cumple que E(X) = 0, se llama juego equitativo, si E(X) > 0 es ventajoso para el jugador y si E(X) < 0 es desfavorable.
Ejemplo: Un juego de apuestas consiste en lanzar un dado. Si sale 1 o 2 ganas 3€; si sale 3, 4 o 5 ganas 6€ y si sale 6 pierdes 20 €. ¿es el juego equitativo?
Respuesta: La variable aleatoria es X = {3, 6, –20} y las probabilidades respectivas serán P = {1/3, 1/2, 1/6}. por lo tanto
E(X)= 3· (1/3) + 6 · (1/2) – 20 · (1/6) = 2/3.
Luego el juego no es equitativo. Es ventajoso para el jugador.
El juego será equitativo si, por ejemplo, X = {3, 6, –24}, es decir, si cuando sale seis pierde 24 €.
No siempre es tan sencillo saber si un juego es o no equitativo. Por ejemplo, en el siguiente:
Problema: Pedro y Juan juegan a cara o cruz a 1 € la partida conviniendo en que jugarán como máximo cinco partidas. Además acuerdan que el juego se acabará o bien cuando Juan lleve la ventaja de un euro o bien cuando Juan tenga la seguridad de que no puede acabar ganando un euro.
¿Cuál es la probabilidad de que Pedro gane en un juego un euro, dos euros, o tres euros en un juego de cinco partidas?
¿Es el juego equitativo?
Solución: Designaremos con P la partida que gane Pedro y con J la partida que gane Juan.
El número resultados del juego que se pueden llegar a jugar será, variaciones con repetición de dos elementos (J y P) tomados de cinco en cinco, esto es: 5RV2 = 25 = 32
El juego acabará en el momento que Juan gane un euro extra, por ejemplo PJJ (y, aunque en esta situación de juego no continúen jugando, a efectos de cómputo de los 32 posibles resultados representa cuatro posibilidades: PJJJP, PJJPJ, PJJPP y PJJJJ ).
Contando las posibilidades tenemos que Juan ganará:
1º.- En todos los resultados de partida que comiencen por J (Juan comienza ganando y, una vez ganado el euro se acabó el juego). Hay 24 = 16 juegos que empiezan por J.
2º.- En todas las permutaciones que comienzan por PJJ. De esas hay 22 = 4.
3º.- En el caso PJPJJ. Hay una.
4º.- En el caso PPJJJ. Hay una.
En total Juan ganará en 16 + 4 + 1 + 1 = 22 ocasiones de las 32.
Podríamos pensar que el juego no es equitativo porque Juan gana en 22 ocasiones y Pedro sólo gana en las diez restantes (32 – 22 = 10). Pero hay otra cuestión que hay que tener en cuenta y es que Juan sólo puede ganar un euro en cada juego (de cinco partidas), pero Pedro puede ganar 1, 2 y hasta 3 euros por juego.
Pedro gana 3 € en los juegos que empieza ganando las tres primeras partidas PPP que hay 4
Gana 2 € en los juegos que empiecen por PPJP, que hay dos y en los que empiezan por PJPP que hay otros dos, en total 4.
Gana 1 € en los dos casos: PPJJP y en PJPJP.
Pedro ve la variable aleatoria X como X = { –1, 1, 2, 3} con probabilidades respectivas:
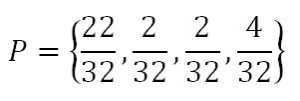
Por lo tanto:
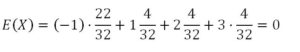
y el juego es equitativo.




