UNA CURIOSIDAD DE LA FUNCIÓN EXPONENCIAL

En el presente trabajo trataremos de analizar lo que sucede cuando se intercambian los papeles de la base y el exponente en una potencia. Es decir, nos preguntamos lo que sucede cuando tenemos dos números reales positivos a y b  y a  <  b  ¿Quién será  mayor a^b o b^a?

Podemos comenzar por ver lo que ocurre con unos ejemplos:

Ejemplo 1:

Con los números 2 < 3, el intercambio de la base y el exponente nos lleva a 2³ = 8  y 3² = 9. Parece indicar que la potencia será mayor cuando el número mayor sea la base  y el menor sea el exponente.

Ejemplo 2.

Tomemos  11 < 12, el intercambio entre la base y el exponente nos lleva a

11¹² = 3.138.428.376.721    12¹¹ = 743.008.370.688

la potencia es mayor cuando el número de la base es menor y   el mayor  sea el exponente.

Ejemplo 3. Si a = 23  y b = 24 se cumple que 24²³  <  23²⁴. Ya que :

23²⁴ =  480250763996501976790165756943041     y   24²³ =  55572324035428505185378394701824

y  24²³ tiene menos cifras que 23²⁴. .  Por lo que, en este caso, la potencia es mayor cuando ponemos el mayor de los números como exponente.

Planteando el problema de forma general:

Sean dos números reales positivos a y b  tales que a < b, si suponemos que se cumple que:    b ^a  <  a ^b  se ha de cumplir lo siguiente:

b ^a  <   a ^b     ⇔     log b ^a  <  log a ^b     ⇔      a · log b  <  b · log a      ⇔

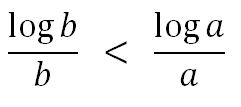Habría que estudiar para valores diferentes el comportamiento de la función:

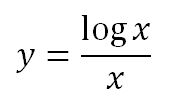Que representada gráficamente es:

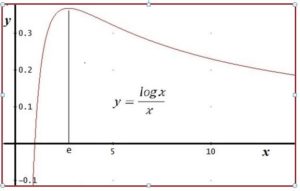
La función tiene las siguientes propiedades

1. – Está definida en el intervalo de los números reales positivos. Dominio = R⁺ = (0, ∞)
2. – Es continua y derivable en su dominio.
3. – Tiene un máximo relativo en x = e. –
4.    Es creciente de (0, e) y decreciente de (e, ∞)

De la gráfica de la función podemos deducir:

a)  Si a y b están en (e, ∞)  y  a < b  entonces, como la función decreciente en esa parte del dominio:

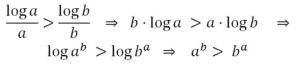lo que signufica que  si a y b ∊ (e, ∞)  y  a < b, entonces  a^b > b^a

b) Si a y b están en (0, e)  y  a < b  entonces:

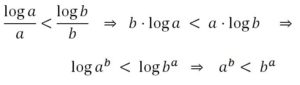lo que signufica que  si a y b ∊ (0, e)  y  a < b, entonces  a^b < b^a

Razonaremos así

1.- Si  tomamos dos elementos a y b pertenecientes el intervalo (e, ∞), si a < b como la función es decreciente en ese intervalo se verifica que:

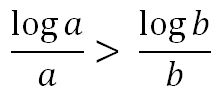por lo tanto          b · log a  >  a · log b    o   log a ^b  >  log b ^a  y, como la función logaritmo es creciente, se cumple que   a ^b  >  b ^a

2.- Si  tomamos dos elementos a y b pertenecientes el intervalo (0, e), si a < b como la función es creciente en ese intervalo se verifica que:

por lo tanto, b · log a  <  a · log b    o   log a ^b  <  log b ^a  , por tanto se cumple que   a ^b  <   b ^a