Peter G. L. Dirichlet (1805-1859) fue profesor en las universidades de Breslau y Berlín. En 1855 sucedió a C.F. Gauss (1877-1855) en la Universidad de Gottinga. Y dio una formulación rigurosa y general del concepto de función como correspondencia entre dos conjuntos, dejando de lado todo lo demás, incluso la regla que relacionaba a los valores de la x con la y. Según sus palabras la correspondencia era lo fundamental del concepto de función y era menos importante el método con el que pudirra haber sido establecida tal correspondencia. El principio del palomar fue formulado por Dirichlet y está relacionado con del concepto de función en una de sus formas más genuinas.
El principio del palomar dice lo siguiente:
- Si n palomas ocupan m nidos y n > m, entonces en un nido habrá al menos dos palomas.
Otra formulación, que proporciona algo más de información, es la siguiente:
- Si se distribuyen am + n palomas en m nidos, y n ≥ 1, entonces habrá algún nido que contenga al menos a + 1 palomas.
Veamos los siguientes ejemplos aritméticos, de aplicación del Principio del Palomar:
Problema 1. A un partido de futbol acuden 740 personas. Demostrar que por lo menos hay tres que cumplen años el mismo día.
Respuesta: Aplicando el principio del palomar considerando:
Palomas: Espectadores = 740, Nidos: Días del año = 365
El principio del palomar nos dice que escribiendo en cada día de un calendario el nombre de un espectador, colocamos los 365 primeros espectadores, acabamos el año y escribimos luego el nombre de los 365 espectadores siguientes, y aún nos quedan 10 espectadores, ya que 740 = 365·2 + 10, luego como mínimo habrá un nido con más de tres palomas (tres personas anotadas en el mismo día).
Problema 2.- Elijamos al azar 60 números enteros distintos de 15 cifras Demostrar que existen dos subconjuntos disjuntos del conjunto de números seleccionados que tienen la misma suma.
Respuesta: Sabemos que con los sesenta números podemos hacer sumas de cero sumandos, de uno, de dos, de tres,… hasta de sesenta sumandos en total:
![]()
Ya que es el desarrollo del binomio (1+1)n = 2n. Por lo tanto podemos realizar hasta 2n. Por lo tanto podemos realizar hasta 260 sumas diferentes.
Los resultados de las sumas no los conocemos, pero si que sabemos que cada número de quince cifras es inferior a 1015 y, como hay 60 números, la suma de los 60 números, que es la cota superior de todas las sumas posibles, será menor a 60 × 1015. Luego quiere decir que no puede haber más de 60 × 1015. sumas diferentes
Para aplicar el principio del palomar tomaremos:
Palomas: cada uno de los subconjuntos del conjunto de los 60 números (260)
Nidos: Cada una de los resultados posibles de las sumas (como máximo 60 × 1015. )
Veamos que hay más palomas que nidos. (Es decir, que 260 > 60 × 1015)
Tomando logaritmos en 260 > 60 × 1015 tenemos:
60 log 2 > log 60 + 15 ⇔ 60 x 0,3010 > 1’7782+15 ⇔ 18,06 > 16’7782, que es cierto.
Se puede probar de otra forma:
210 = 1024 >1000, por tanto:
260 = (210)6 > (103)6 = 1018 = 1000×1015 > 60×1015
Por lo tanto: 260 (número de sumas) > 60 × 1015 (número de resultados)
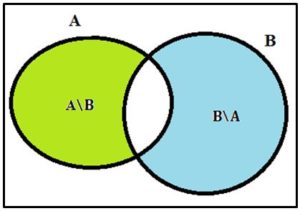
Por el principio del palomar, deben existir dos subconjuntos, A y B, con la misma suma (que es lo que se quería probar), pero esos subconjuntos no tiene por qué ser disjuntos y pueden tener intersección no nula. Sin embargo los conjuntos A\B y B\A son disjuntos, como se ve en la figura:
Problema 3. Dados 2019 números enteros distintos cualesquiera. Probar que siempre podemos encontrar dos de ellos cuya diferencia sea divisible por 2018.
Respuesta: En este caso las palomas van a ser los 2019 números y los nidos serán los restos que se obtienen al dividir cada uno de los números por 2018, es decir, los nidos serán los números 0, 1, 2,…, 2017.
Por lo tanto, tenemos 2018 restos (nidos) posibles para las 2019 números (palomas), llamaremos a estos números
a1, a2, a3, …., a2019
Con 2019 números, por el principio del palomar, podemos asegurar que habrá, al menos, dos de ellos que den el mismo resto al dividirlos por 2018, por ejemplo, supongamos que a1 y a2 tienen el mismo resto al dividirlos por 2018, entonces la diferencia de estos dos números a1 – a2 es dará resto cero al dividirlos por 2018 por lo tanto a1 – a2 será divisible por 2018, que es lo que queríamos probar.
Problema 4.- Demostrar que existen números con todas las cifras iguales que son múltiplos de 29.
Respuesta: Consideremos los treinta números, formados por unos:
1, 11, 111,…, 11…30 cifras..1 [1]
Llamemos a los números a1, a2, a3,….., a30 respectivamente
Si alguno de esos treinta números fuera múltiplo de 29, el problema ya estaría resuelto, ya que ese sería el número que buscamos. Veremos que uno de ellos será divisible por 29:
Sabemos que cuando se divide cualquier número entre 29 sólo puede dar uno de los siguientes veintinueve restos diferentes:
0, 1, 2, …., 28
Por lo tanto, entre los restos obtenidos en las divisiones de los treinta números de [1] entre 29 debe haber al menos dos restos iguales. Sean los números que dan restos iguales:
aj = 11… j cifras …1 y ak = 11… k cifras…1 y j > k
La diferencia de ambos será un número formado por j-k unos y k ceros que será divisible por 29:
aj -ak = x = 11… j –k cifras … 100…. k cifras ….0
El número x es múltiplo de 29, pero no tiene las cifras iguales como nos exige el enunciado. No obstante, admite la descomposición en el producto de los dos factores
x = 11 … j –k cifras … 1 x 100… k cifras … 0
Como 29 divide a x y no divide al factor 100… k cifras … 0 (ya que sólo tiene como factores primos el 2 y 5), por lo tanto, necesariamente dividirá al otro factor, es decir a:
11… j –k cifras … 1
Que es un número de la lista formado por cifras j-k iguales, es decir, el número aj-k, que tiene j-k unos y será divisible por 29.