La partición de un triángulo equilátero en otros triángulos equiláteros menores, tiene una serie de propiedades curiosas, algunas de ellas las vamos a recoger en el siguiente artículo en una serie de apartados.
DIVISIÓN EN TRIÁNGULOS EQUILÁTEROS IGUALES
PRIMERO. – ¿Se puede dividir un triángulo equilátero en 20 triángulos equiláteros iguales?

Respuesta: Cada vértice del triángulo equilátero de partida, ABC, tiene que ser vértice de uno de los triángulos equiláteros menores que constituyen la partición. Por ejemplo, el vértice B; si ABC tiene lado L, el triángulo pequeño debe tener un lado L/n (en la figura L/4), para que la base A’B de A’BC’ quepa un número entero de veces en la de AB deABC. La razón de semejanza entre los triángulo ABC y A’BC’ será 1/n y la razón entre sus áreas 1/n2. Por lo tanto, en el triángulo ABC caben exactamente n2 triángulos del tamaño A’BC’.
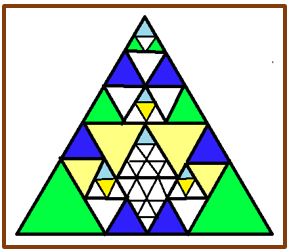
Por consiguiente, cualquier triángulo equilátero ABC se sólo se puede dividir en un número cuadrado de triángulos equiláteros. Como 20 no es cuadrado perfecto, no se puede dividir en veinte de triángulos equiláteros iguales. Sin embargo, se puede dividir en triángulos equiláteros desiguales como se muestra en la figura: en la que hay 1, 3, 7 y 9 triángulos equiláteros de la primera a la última fila.

SEGUNDO. – Si dividimos los tres lados del triángulo equilátero de lado L en n partes iguales y trazamos por cada punto de división paralelas a los otros lados: ¿Cuántos triángulos equiláteros de lado L/n hay en la última fila?

Respuesta: La primera fila, la del vértice superior hay 1. En la fila enésima, está entre dos rectas paralelas, la inferior dividida en n partes, que son las bases de n triángulos, la superior está dividida en n-1 partes que son las bases de n-1 triángulos, luego contiene
n + (n-1) = 2n-1 triángulos equiláteros.
Con razonamiento análogo la fila k tendrá 2k – 1 triángulos. Por lo tanto, se puede constatar de nuevo que el número de triángulos equiláteros iguales en los que se puede dividir un triángulo equilátero será:

TERCERO. – ¿Es posible dividir un triángulo equilátero en 5 triángulos equiláteros (aunque sean de diferente tamaño)?

Respuesta: Cada vértice del triángulo equilátero de partida, ABC, tiene que ser vértice de uno de los triángulos equiláteros menores que constituyen la partición. El triángulo ABC no puede dividir en menos de cuatro triángulos equiláteros.
Partamos del vértice B, y, a partir de él, el triángulo equilátero BDE (DE paralela a la base AC)
El trapecio ADEC, no se puede dividir en cuatro triángulos equiláteros. (En el ángulo ADE de 120º entran, necesariamente, dos triángulos equiláteros igual que en el ángulo DEC). Entonces el trapecio ADEC admite como división con número mínimo de cinco triángulos equiláteros.
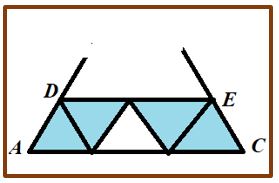
Que, junto con el triángulo BDE hacen seis triángulos. El razonamiento se podría resumir:
Se podrían formar tres, (sin dividir la base menor) lo que nos llevaría a dividir el triángulo equilátero en cuatro triángulos.
Pero en cualquier otro caso, teniendo en cuenta que en el ángulo ADE de 120º entran, necesariamente dos triángulos equiláteros, habrá k triángulos con un vértice hacia abajo y base en la base menor del trapecio y k +1 con el vértice hacia arriba y base en la base mayor del trapecio. Entonces se cumple en el trapecio habrá siempre
(k+1) +k = 2k+1 triángulos equiláteros, que es un número impar. Lo que significa que en el trapecio se formarán un número impar de triángulos.
CUARTO. – Demostrar que cualquier triángulo equilátero se puede dividir en n triángulos equiláteros, para cualquier numero natural n > 5.
Respuesta:
- Un triángulo equilátero se puede dividir en cuatro triángulos equiláteros iguales trazando las tres paralelas medias.
- Podemos dividir un triángulo equilátero en seis, siete y ocho triángulos como se muestra a continuación:
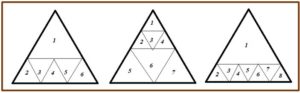
A partir de la división de un triángulo equilátero en seis triángulos equiláteros, podemos dividir sucesivamente uno de los triángulos menores en cuatro partes iguales, con lo cual incrementamos en cada paso el número de triángulos en tres. Y, en n pasos, dividimos el triángulo original en ⇒ 6 + 3n = 3(n+2), que es un múltiplo de tres. Dividimos el triángulo original en
A partir de la división de un triángulo equilátero en siete triángulos equiláteros, podemos dividir sucesivamente uno de los triángulos menores en cuatro partes iguales, con lo cual incrementamos, en cada paso, el número de triángulos en tres. Y, en n pasos, dividimos el triángulo original en ⇒ 7 + 3n = 3(n+2) +1, que es un múltiplo de tres más uno.
A partir de la división de un triángulo equilátero en ocho triángulos equiláteros, podemos dividir sucesivamente uno de los triángulos equiláteros menores en cuatro partes iguales, con lo cual incrementamos, en cada paso, el número de triángulos en tres. Y, en n pasos, dividimos el triángulo original en ⇒ 8 + 3n = 3(n+2) +2, que es un múltiplo de tres más dos.
Podemos dividir un triángulo equilátero en un múltiplo de tres, en un múltiplo de tres más uno y en un múltiplo de tres más dos. Es decir, en cualquier número de triángulos equiláteros.