Estudio matemático de las poblaciones analiza la variación del número de individuos, a través del tiempo, que depende de factores variados como las tasas de natalidad y de mortalidad, el número de individuos fértiles o los recursos medioambientales. El estudio de la evolución de las poblaciones tiene especial interés para los biólogos, para los gobiernos naciones y para las compañías de seguros.
Un ejemplo matemático del crecimiento demográfico fue expuesto por el economista británico Th. Malthus (1776−1834) en su obra Ensayo sobre el principio de la población (1798), en la analizaba que la causa de la miseria en el mundo era que no se ajustaba el crecimiento de la población a la producción de alimentos en el mundo, ya que, mientras que los alimentos crecían según una progresión aritmética la población aumentaba en progresión geométrica, siguiendo una ley exponencial. Además añadía que los factores de regulación natural de la población, como las guerras, las catástrofes naturales o las epidemias eran factores que sólo retrasaban lo inevitable, que era la hambruna mundial en un futuro más o menos próximo.
La solución al problema pasaba por construir una sociedad que controlara la natalidad. Pero detrás de esta idea, de carácter social global, estaba una clase social perjudicada: la de los pobres, que, a juicio de Malthus, era la responsable de su propia pobreza por reproducirse tanto. La pobreza era responsabilidad de cada uno de los propios individuos y no dependía, por tanto, del sistema económico. La teoría malthusiana de la población fue soporte teórico o inspiración para otras teorías relacionar el crecimiento demográfico y sus consecuencias sociales.
Esta idea de sociedad formada por elementos individuales que labraban su propia suerte la adoptó Darwin en el Origen de las Especies (1859) al poner en la base de la evolución la selección natural mediante la lucha por la vida de cada individuo.
El modelo malthusiano de crecimiento de la población, afirma que la velocidad de crecimiento de una población que en un instante t tiene P(t) individuos es proporcional a población, es decir, que cimple la ecuación diferencial:
P´(t) = k · P(t) (k > 0) ⇒ P(t) = C · e kt (1)
Quizás la verdadera influencia de la obra de Malthus no esté tanto en las aportaciones a los estudios puramente demográficos de evolución de poblaciones, sino en centrar la mirada en el problema de la distribución de los recursos disponibles entre la población, que llevó a establecer la relación entre crecimiento demográfico y desarrollo económico.
La ecuación de Malthus apuntaba un crecimiento exponencial que, en el caso de k > 0, hacía que la población tendiera a infinito, pero ese no era el comportamiento de las poblaciones que se observaban. Porque para los estudios de poblaciones, es cálculo de cuotas de seguros de vida sería más realista hacer que la velocidad de crecimiento, P´(t), fuera disminuyendo progresivamente. En esta línea aparecieron diferentes ecuaciones para describir la evolución de la población a lo largo del tiempo. La mayoría de ellas partían de la idea de ralentizar la velocidad de crecimiento de Malthus.
En 1825 el matemático inglés B. Gompertz (1779-1865) introdujo la ecuación:
En la que se modificaba la velocidad de crecimiento malthusiana a medida que crecía población. Integrada la ecuación diferencial daba lugar la función:
que fue utilizada por W.M. Makeham (1826-1891) en las compañías de seguros para calcular cuota de cada edad para hacer seguros de vida.
Pero la función matemática que más interés despertó para cálculos de poblaciones futuras fue la conocida con el nombre de logística. La idea de esta ecuación arranca del matemático, estadístico y astrónomo belga A. Quetelet (1796-1874), que en su empeño de aplicar las matemáticas a las ciencias sociales, e influido, seguramente, por la mecánica newtoniana se la caída libre de un cuerpo teniendo en cuenta la resistencia del aíre: ma = – mg + kv2 que es equivalente a v’ = – g + (k/m)·v2, planteó en 1835 la idea de que la velocidad de crecimiento de una población, P(t), debía estar sometida a una resistencia proporcional al cuadrado de dicha población. La idea fue recogida por un antiguo alumno suyo, llamado P. F. Verhulst (1804-1849) y lo publicó en un artículo titulado: Noticia sobre la ley que sigue la población en su crecimiento (1838).
Verhulst tenía la idea de que en la ecuación de Malthus la velocidad de crecimiento de la población P(t) debía estar frenada por una función f (t) y aplicó la sugerencia de Quetelet de que esa función debía ser f (t) = n·P 2 (t)
P’(t) = k· P(t) – n·P 2 (t)
Que integrada resulta:
El cálculo de la población con esta fórmula depende de tres constantes, k, n y la cte. de integración. Conociendo la población en tres momento distintos podemos calcular las constantes y tendremos una ecuación con la que podemos calcular la población en un momento cualquiera.
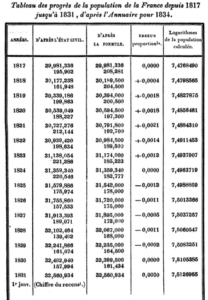
Comprobó con el anuario de 1834 que la población entre 1817 y 1831 había aumentado siguiendo la ley que él había descubierto, como se puede apreciar en el caso de la población de Francia:
Las constantes de la ecuación logística tienen un significado como puede observarse transformando la ecuación de la siguiente forma:
La velocidad de crecimiento de una población será nula cuando:
P (t) = 0 o P (t) = k/n = K
Es decir, cuando no hay población o alcanza la población máxima, K, que puede alcanzar el hábitat dónde se desarrolla la población y la podemos escribir:
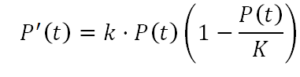
Integrando la ecuación obtenemos la función:
Donde C es la constante de integración y es necesario conocer tres valores de la población en momentos diferentes para determinar K, C y k. La expresión de la población contiene la función exponencial, pero su crecimiento no es indefinido como sucede en el modelo Malthusiano, la población está acotada por el valor K. Como se indica en la gráfica:
La obra de Verhulst y, en consecuencia, la ecuación logística, permaneció en el olvido hasta el año 1920, en que los matemáticos americanos R. Pearl (1879-1940) y L.J. Reed (1886-1966) escribieron una serie de artículos sobre el crecimiento de poblaciones y llegaron la ecuación que Verhulst había empleado casi un siglo antes y aplicaron la ecuación logística para predecir la población de los Estados Unidos en el año 2000 mediante su ecuación y anunciaron una población de 185 millones de habitantes. No acertaron porque ese año Estados Unidos alcanzó una población de 260 millones de habitantes. La ecuación de Verhulst no se ajusta bien a situaciones reales habituales, pero es buen modelo para el estudio del crecimiento de poblaciones bajo restricciones y con recursos limitados.
La ecuación logística ha alcanzado una gran popularidad, porque, además de ser un modelo aceptable para la evolución de cierto tipo de poblaciones, es, en su forma discretizada:
xn+1 = A·xn·(1 – xn)
un modelo sencillo del comportamiento caótico de los sistemas no lineales.
