La ecuación logística está ligada al estudio de la evolución de poblaciones y viene a modificar el modelo propuesto el economista británico Th. R. Malthus (1766-1834), que publicó, en 1798 una obra titulada Ensayo sobre el principio de la población referida a la sociedad humana y su evolución. Malthus enunció una ley según la cual la población siempre tendía a crecer más rápidamente que la producción de alimentos; un aumento de la producción de éstos debía inducir un crecimiento de la tasa de reproducción en la población y concluyó que las poblaciones debían estar siempre sometidas a las hambrunas y otras calamidades, que limitaran el número de individuos. Los modelos de crecimiento de población derivados del pensamiento maltusiano son esencialmente:
1.- El modelo maltusiano exponencial en su forma más simple, que supone que las poblaciones se reproducen de forma ideal sin que exista ningún factor de corrección que limite su crecimiento vegetativo, las poblaciones crecen en progresión geométrica y los alimentos en progresión aritmética.
2.– El modelo logístico, que es una corrección del anterior y supone que sobre las poblaciones actúan algunos factores que limitan su crecimiento tales como depredadores, alimentos limitados, enfermedades, etc y a ellos adaptan su crecimiento.
CRECIMIENTO MALTUSIANO EXPONENCIAL
Lo expondremos con un ejemplo: supongamos que una colonia de insectos, bacterias o virus tiene un ciclo de vida anual (cada individuo vive un año) y que cada hembra engendra, en promedio, un número k de hembras reproductoras viables al año siguiente y muere.
Si P0 es el número de hembras iniciales, al acabar el primer año habrá P1 = k P0 al acabar el segundo habrá N1 = k N1 y así sucesivamente. El proceso lo podemos expresar así:
Población inicial : P0
Primer año: P1 = k P0
Segundo año: P2 = k P1 = k2 P0
……………………………..
A los n años: Pn = k Pn-1 = kn P0
El modelo anterior se puede expresar en lenguaje funcional. El número de individuos de la población es función del tiempo, si tenemos en cuenta que:
P0 (Población inicial) = P(0) (Población en el instante 0)
P1 (Población en el instante 1) P(1) = k· P(0)
…………………………………………
En un instante t cualquiera la población será: P(t) = k t· P(0) .
Las gráfica de esta función, P(t) = P(0)·k t, para distintos valores de k es como sigue:

EL CRECIMIENTO LOGÍSTICO
La evolución de una población en un medio físico real está fuertemente condicionada por una serie de factores que limitan el crecimiento exponencial de Malthus. El peso de las limitaciones impuestas por el medio, por ejemplo alimenticias, serán escasas mientras la población sea muy pequeña, pero se dejarán notar a medida que la población crezca. Estas limitaciones harán que se haga más lento el crecimiento cuando la población sea grande. Una población, situada en un medio físico real que la limita y sometida a un conjunto de condicionantes, en principio constantes y el número de individuos podrá acoger como máximo, en las condiciones más favorables posibles, un valor máximo M que, en general, es desconocido.
Cuando la población está muy por debajo del valor máximo evolucionará según el modelo de Malthus, pero, a medida que la población se acerque al valor M, crecerá más despacio; y si la población llegara a alcanzar ese valor, la tasa de crecimiento sería nula.
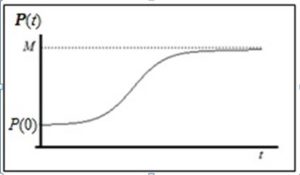 Una gráfica de este tipo se produce, cuando se modifica el crecimiento exponencial Maltusiano: Pn = kn ·P0 de la siguiente forma:
Una gráfica de este tipo se produce, cuando se modifica el crecimiento exponencial Maltusiano: Pn = kn ·P0 de la siguiente forma:
![]() con A > 0, B > 0, k > 0, a < 0
con A > 0, B > 0, k > 0, a < 0
Para obtener esta ecuación multiplicamos el segundo miembro de la ecuación de crecimiento exponencial malthusiano, Pn = k Pn-1 , por un factor que depende de M. En concreto se impone la condición de que el número de individuos sea cada año proporcional al número de individuos que tiene la población y al número de individuos que le faltan para alcanzar el valor máximo M, esto es:
Pn+1 = k Pn (M – Pn)
Expresión que nos da la relación entre la población de una generación y la siguiente. Se puede observar que a medida que la población se acerca al valor de M crece más despacio y toma la forma representada en la gráfica anterior.
Se llama ecuación logística en forma canónica a: xn+1 = k xn (1 – xn)
Esta ecuación representa la evolución de una población a lo largo del tiempo en la que la población máxima es M = 1 y las xn son fracciones de población, es decir, que xn= 1/2 quiere decir que la población será Pn=M/2 por consiguiente xn sólo puede tomar valores comprendidos entre 0 y 1.
Para que la ecuación logística en forma canónica xn+1 = k xn (1 – xn) represente un modelo de evolución de poblaciones la constante k no puede tomar un valor cualquiera. Veremos a continuación que los valores admisibles de k en la ecuación en forma canónica pertenecen están comprendidos entre 0 y 4.
Las xn no pueden tomar valores negativos ni mayores que 1, por lo tanto, k > 1, luego:
o ≤ xn+1 = k xn (1 – xn) ≤ 1 ⇒ xn (1 – xn) ≤ 1/k (1)
La función xn (1 – xn) alcanza el valor máximo cuando xn = 1/2, por (1)
![]()
Luego 0 ≤ k ≤ 4
Nota: En realidad, hemos calculado el máximo absoluto de la función y = k x(1 – x) en el intervalo [0,1]. La función se anula en los extremos del intervalo, luego el valor máximo lo alcanza en el valor de x que verifica: y’ = -2x +1 = 0 ⇒ x = 1/2. Por lo tanto, los valores admisibles de k están comprendidos entre 0 y 4, ambos incluidos.
COMPORTAMIENTO DE LA ECUACIÓN LOGÍSTICA SEGÚN LOS VALORES DE k
Los trabajos principales en dinámica de poblaciones se deben al ingeniero, matemático y físico convertido en biólogo Robert May (1938-) y que estudió de forma especial la ecuación logística.
La ecuación logística tiene una representación en función del tiempo que difiere en su forma según los valores del parámetro k. Se puede dibujar sin más que calcular los valores de la población para los instantes t = 0, t = 1, t = 2 , t = 3, .., que serán P(0), P(1), P(2), P(3), … representar los puntos (0, P(0)), (1, P(1)), (2, P(2)), (3, P(3)), …. .
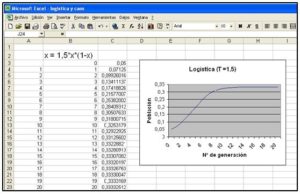
Representación de xn+1 = 1,5 xn (1 – xn) [k =1,5]
Supongamos que comenzamos con una fracción de población x0 = 0,05. Se ha calculado el valor de la población en generaciones sucesivas con la Hoja de Cálculo obteniéndose la Tabla de valores y su representación:
PUNTOS FIJOS DE LA ECUACIÓN LOGÍSTICA
Al estudiar la evolución en el tiempo de una población gobernada con la ecuación logística, para algunos valores del parámetro k se observa un fenómeno notable: la población alcanza un determinado valor, a, y, a partir de ese valor ya no cambia y permanece fijo en sucesivas generaciones. En esas circunstancias se cumple que: xn+1 = xn o x (t +1) = x(t).
Para determinar los puntos fijos haciendo xn+1 = xn = a y calculemos a.
a = ka (1 – a) ⇒ 0 = k a – ka2 – a ⇒ 0 = a (k-1) – ka2 ⇒
⇒ 0 = a [(k-1) – ka] ⇒
![]()
La población alcanza un punto fijo cuando adquiere cualquiera de los dos valores anteriores.
Pero la ecuación logística presenta comportamientos diferentes según los valores de la constante k . A continuación exponemos los siguientes situaciones:
1.– Cuando 0 ≤ k < 1, independientemente del valor inicial Po del que partamos, la población tiende asintóticamente a cero, es decir, que la población se extinguirá en unas pocas generaciones.
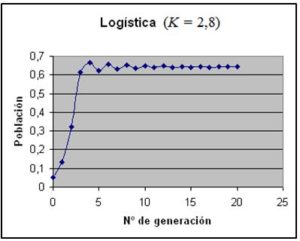
2.– Para 1 ≤ k < 3 se observa que la población tiende al punto fijo (k – 1) /k, con independencia del valor inicial que tomemos. A continuación damos la representación para k = 2,8, que tiende al valor fijo a = 0,6429.
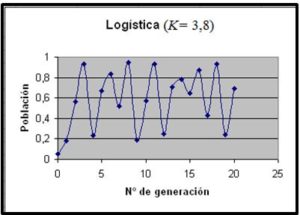
3.- Cuando 3 ≤ k < 3,449 el punto fijo se hace inestable y la población oscila alternativamente entre dos valores fijos estables, como se observa en la gráfica siguiente:

4.- Cuando 3,449 < k < 3.56994546, se observa que la población final oscila entre cuatro, ocho, dieciséis, … , o 2n valores, presentando la gráfica aspectos como el siguiente, que oscila entre cuatro valores

5.– Cuando 3,56994546… < k < 4 aparece el comportamiento caótico. Y la gráfica oscila de forma irregular e imprevisible y dependiendo del valor inicial con el que se inicia la iteración, como en la siguiente gráfica;