Definición: Progresión Aritmética de números reales es una sucesión en la que cada uno de sus términos se obtiene sumándole un número fijo al término anterior. Al número fijo se le llama diferencia y se designa con d.
En una Progresión Aritmética a1, a2, a3, . . ., an, … se cumple, por tanto, que an = an-1 + d. Y el término general se puede expresar en función del primer término y de la diferencia d de la siguiente forma: an = a1+ (n-1) d.
Estas sucesiones se llaman Progresiones Aritméticas de Primer Orden o simplemente Progresiones Aritméticas.
Observación 1: El término general de una Progresión Aritmética de Primer Orden es un polinomio de primer grado en n. Esto es: an = P1(n) = an + b, Donde a = d, b = a1 – d y n indica el número de orden de cada término en la Progresión
Definición: Una Progresión Aritmética de Segundo Orden es una sucesión numérica cuyo término general es un polinomio de segundo grado en n, es decir: an = P2(n) = an2 + bn + c
Observación 2: Así como en las Progresiones Aritméticas de Primer Orden la diferencia entre dos términos consecutivos es constante, en las Progresiones Aritméticas de Segundo Orden, las sucesivas diferencias de términos consecutivos forman una Progresión Aritmética de Primer Orden
Para probarlo basta ver que la diferencia entre dos términos consecutivos cualesquiera es un polinomio de primer grado en n
an – an-1 = an2 + bn + c – [a(n-1)2 + b(n–1) + c] =
= an2 + bn + c – [an2 -2an + a + bn – b + c] =
= an2 + bn + c – an2 + 2an – a – bn + b – c = 2an + (b – a)
Que es de primer grado en n.
Ejemplo: La Progresión de término general an = P2(n) = n2 + n + 1 se puede escribir 3, 7, 13, 21, 31, 43, 57, 71…. Y la diferencia de términos sucesivos es una progresión aritmética de razón dos 4, 6, 8, 10, 12, 14… Se suele escribir y queda claramente reflejado así:

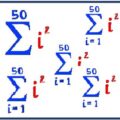
PROBLEMA 1. Hallar la suma de los veinte primeros cuadrados, de la progresión aritmética 2, 5, 8, 11, 14. 17 …
Solución: Comprobaremos que la que la sucesión formada por los cuadrados de los términos de la Progresión Aritmética son un Progresión Aritmética de Segundo Orden, como se comprueba en la siguiente tabla:

Por lo tanto, su término general será de la forma P2(n) = an2 + bn + c, este término general lo calcularemos por el método de coeficientes indeterminados que da lugar al sistema de ecuaciones tres ecuaciones con tres incógnitas:
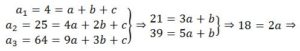
a = 9 , b = -6 y c = 1, por tanto cn = 9n2– 6n +1
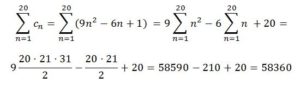
Otra forma de calcular el término general de la sucesión de los cuadrados de los términos de una progresión aritmética se expone en problema siguiente:
PROBLEMA 2.- Halla la suma de los cuadrados de los cien primeros términos de la progresión aritmética: 2, 5 ,8, 11, 14, 17…
Solución: La sucesión tiene de término general an = 2 + 3(n-1). El cuadrado de los términos de la progresión aritmética dada será una progresión aritmética de segundo orden, ya que: la sucesión 4, 25, 64, 121, 196, 324,… tiene de termino general:
cn = (an)2 =(2 + 3(n-1))2 = 4 + 9 (n-1)2 + 12(n-1) = 9n2 – 6n + 1
La suma de los cien primeros términos se realiza como en el caso anterior (utilizando las fórmulas de los n primeros números naturales y la de la suma de los cuadrados):