El Teorema de Pitágoras será, seguramente, el teorema más popular de las matemáticas y el que más demostraciones diferentes ha tenido. En el libro de E. Scott Loomis (1968) The Pythagorean Proposition se recogen alrededor de trescientas setenta pruebas del mismo con sus correspondientes figuras y comentarios.
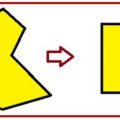
Por esta razón no voy a intentar destacar algunas demostraciones sobre todas las demás. Unas denotan gran ingenio, otras sobresalen por la belleza de la figura y otras asombran por su simplicidad. Muchas de ellas son demostraciones simples que se deducen de la simple observación de la figura geométrica empleada para razonar. Por ejemplo:

Donde se puede observar en que la suma de las áreas de los dos cuadrados en verde de la izquierda es igual al área del cuadrado verde de la izquierda, con lo que se prueba que: a2 + b2 = c2 . Es decir se demuestra el Teorema de Pitágoras.
Desde que se descubrió el cálculo aritmético-algebraico, hacia el siglo XII, se utilizaron métodos y razonamientos mixtos. Un lenguaje entre algebraico y geométrico parecido al siguiente:
Un cuadrado tiene de lado a + b, por tanto su área es:
A = (a+b) (a+b) = a2 + 2ab + b2
Haciendo la descomposición según el cuadrado de la izquierda:
![]()
Haciendo la descomposición según el cuadrado de la derecha:
![]()
De (1) y (2) se deduce que
a2 + b2 = c2
Resulta curioso que alguna demostración tan sencilla como ésta no surgiera en la Escuela Pitagórica, ni fuera recogida en los Elementos de Euclides, el cual en la obra optó por una demostración bastante más compleja y difícil basada en la igualdad de áreas que resultaba menos directa e intuitiva. Así el teorema de Pitágoras se ganó en las Escuelas Medievales el apelativo de Pons asinorum (puente de asnos). Términos con los que se designaba la gran dificultad que se encontraban los estudiantes en dificultad en el aprendizaje de la Geometría. Y era utilizado como prueba para evaluar los conocimientos matemáticos de estudiantes. El obstáculo no se explica por la gran cantidad de demostraciones que se han realizado del mismo, sino porque el teorema está colocado al final de una cadena de deductiva que constituye el primer libro de los Elementos. El Teorema de Pitágoras aparece en las dos últimas proposiciones (Proposiciones 47 y 48) del Libro primero de los Elementos de Euclides como consecuencia final obtenida de los resultados deducidos anteriormente
Teorema: «En los triángulos rectángulos, el cuadrado construido sobre el lado que subtiende el ángulo recto es igual a la suma de los cuadrados sobre los lados que contienen dicho ángulo».
Habitualmente el Teorema de Pitágoras se enuncia: el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Demostración: (Siguiendo los Elementos de Euclides, en la que destacaremos el carácter axiomático deductivo de la Geometría señalando, en algunos pasos del razonamiento, los postulados, principios y proposiciones anteriores en los que se basan diferentes pasos de la demostración. Precisamente esta concatenación secuencial y la coherencia lógica del conocimiento geométrico manifestadas en el libro fue lo que hizo que la Geometría de los Elementos fuera el lugar seguro y riguroso del conocimiento matemático y se mantuviera como obra de referencia del saber matemático durante más de veinte siglos)
Euclides demostró el teorema así:
Sea el triángulo ABC, rectángulo en A. Veremos que el cuadrado construido sobre BC es igual a la suma de los cuadrados construidos sobre AB y AC. Dibújese sobre CB el cuadrado CDHI, sobre AB el cuadrado ABGF y sobre AC el cuadrado ACDE [Proposición 46].
1.- Los triángulos CDB y CAI son iguales, ya que tienen dos lados iguales e igual el ángulo obtuso comprendido (los ángulos obtusos son iguales puesto que ambos son iguales a un recto más el ángulo ACB y los lados que los forman son iguales por ser lados de cuadrados).
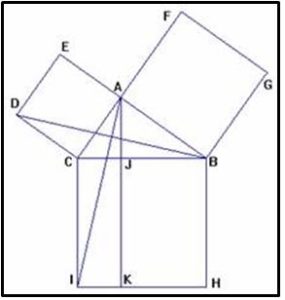
2.- El área del triángulo CDB es igual al área del triángulo ACD, (tienen la misma base, CD, y la misma altura) [Proposición 4] y es la mitad del cuadrado ACDE .
3.- El área del triángulo CAI es igual a la mitad de la del rectángulo CJKI (tienen la misma base CI y la misma altura, CJ)
Por tanto, el área del cuadrado ACDE es igual al área del rectángulo CJKI. Por el mismo procedimiento se demuestra que el área del cuadrado AFGB es la misma que la del rectángulo JBHK y, por lo tanto, el cuadrado construido sobre BC es igual a la suma de los cuadrados construidos sobre AB y AC
Por otra parte, es de destacar que Euclides escribe a continuación la Proposición 48 que es el enunciado del teorema recíproco. En realidad esta proposición era la que, en la práctica, utilizaban desde la antigüedad los agrimensores egipcios para el trazado de perpendiculares mediante una cuerda de 12 nudos separados a distancias iguales.
Proposición 48.– «Si en un triángulo el cuadrado construido sobre uno de los lados es igual a la suma de los cuadrados construidos sobre los otros dos lados del triángulo, el ángulo formado por estos dos lados es un ángulo recto».

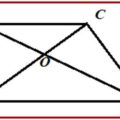
Demostración: Supongamos que en el triángulo ABC se cumple el Teorema de Pitágoras, esto es que:
CB2 = AC2 + AB2
Trazamos una semirrecta AE perpendicular al lado AC y en ella señalamos el punto D tal que AD = AB.
Los triángulos ABC y ADC son iguales, puesto que tienen el lado AC común. También AD = AB por construcción. Además como el triángulo CAD es rectángulo se puede aplicar el Teorema de Pitágoras, por tanto:
CD2 = AC2 + AD2, como AD = AB ⇒ AC2 + AB2,
y como suponemos que el triangulo ABC cumple el teorema de Pitágoras:
AC2 + AB2 = CB2
Como los triángulos ABC y ADC son iguales y ADC es rectángulo en A, también lo será el triángulo ABC, como queríamos demostrar.
En suma, la demostraciones de Euclides de que todo triángulo rectángulo cumple el Teorema de Pitágoras y que, recíprocamente, si cumple un triángulo cumple el Teorema de Pitágoras es rectángulo aportan más que la simple demostración visual. Coloca una propiedad dentro de un sistema deductivo en el que cada paso se apoya en una regla lógica, en un axioma o en una proposición anteriormente probada.