Los polígonos estrellados han sido muy utilizados a lo largo de la historia. Los Pitagóricos adoptaron el pentágono estrellado (pentalfa) como emblema de su hermandad y los musulmanes los han empleado profusamente en su decoración geométrica de mosaicos, bóvedas y frisos, sobre todo el pentágono estrellado octogonal.
En este trabajo haremos un estudio matemáticos sobre algunas características geométricas de estos polígonos.
Los polígonos se pueden clasificar en cóncavos y convexos. Los polígonos cóncavos son aquellos que tienen, al menos, un ángulo interior de más de 180°. Por consiguiente, los polígonos cuyos ángulos interiores son todos menores de 180º son convexos
Un polígono estrellado es regular cuando es cóncavo, y sus ángulos interiores y sus lados son iguales.
Si una circunferencia se divide en m partes y los puntos de división (vértices) se unen sucesivamente, se obtiene un polígono convexo, pero si se unen los vértices de dos en dos, de tres en tres en 3, … de p en p, los polígonos que aparecen son cóncavos y estrellados.
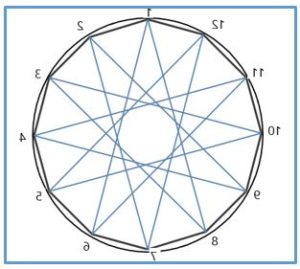
Si dividimos una circunferencia en doce partes iguales (m = 12) y unimos los vértices de cinco en cinco (p = 5), recorremos la circunferencia de la siguiente forma 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8, 1 en doce pasos. Se cierra la poligonal después de recorrer la circunferencia un número entero de veces, el resultado será un polígono regular estrellado (o de especie superior).
Se llama orden de un polígono estrellado al número de lados (doce) y especie al número de vueltas que se da a la circunferencia al recorrer su contorno (cinco) 5×30 x 12 (quinta especie)
Recapitulando: para construir un polígono estrellado se procede como sigue:
1º.- Se divide la circunferencia en m partes iguales de amplitud αº = 360º/m y unimos los puntos de división (vértices) de p en p.
2º.- Las cuerdas trazadas, que subtienden ángulos de pαº, son los lados del pentágono estrellado (cada lado contiene p particiones m-ésimas de la circunferencia)
3º.- Para que el polígono estrellado de n lados se cierre es necesario que npα sea igual a 360º o a un múltiplo de 360º (es decir, número entero de veces, q, 360º, q·360º), luego se tiene que verificar la igualdad:
npα = qmα
El número de lados n será:
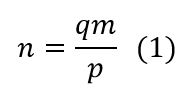
Donde q será el menor entero que hace que el cociente sea entero.
Se pueden dad los siguientes casos:
Caso 1º.- Que m sea múltiplo de p.
En este caso, como q es el menor entero que hace que el cociente (1) sea entero, q debe ser igual a uno y, por lo tanto, n = m / p y el polígono será de primera especie y convexo.
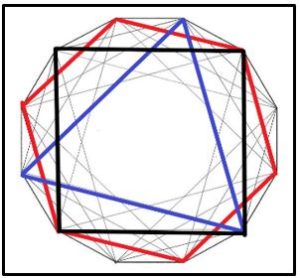
Los comprobamos con el siguiente ejemplo. Dividimos la circunferencia en m = 12 partes. Como p es divisor de m, p puede ser 1, 2, 3 o 4 y se unen de uno en uno (dodecágono), de dos en dos (hexágono), de tres en tres (cuadrado)y de cuatro en cuatro (triángulo equilátero) (Para p = 6 sería un diámetro)
Caso 2º.- Que m y p sean primos entre sí,
En este caso Como m y p primos entre si, y n debe ser entero el menor valor de q debe ser p, por lo tanto (simplificando), n = m (Tantos lados como particiones). Polígono de m lados recorrido p veces
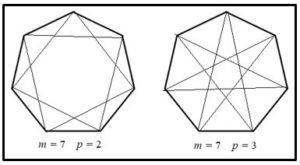
Ponemos el siguiente ejemplo para m = 7 y p = 2 da un heptágono estrellado que recorre dos veces la circunferencia ( de segunda especie) y para m = 7 y p=3 heptágono estrellado que recorre tres veces la circunferencia (de tercera especie)
Caso 3º.- Que m y p tengan factores comunes, es decir, que d = mcd (m, p) ≠1,
Sea m = d·m’ y p = d· p’. mcd (m’, p’) =1, lo que implica que:
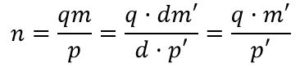
Como m’ y p’ son primos entre si el menor valor posible de q será p’, resultando que n = m’ y obtendremos un polígono de m’ lados que recorre la circunferencia p’ veces. Se forma un polígono de género m/r y especie p/r
Ejemplo: Se puede observar en el pentadecágono m =15 = 3·5, cuando se unen los vértices de 6 en 6, p = 6 =2·3. En este caso m’ = 5 y p’ = 2 y uniendo los vértices de seis en seis se obtiene el polígono estrellado de cinco puntas que recorre la circunferencia dos veces
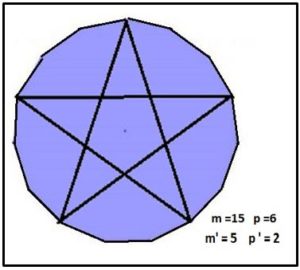
En consecuencia, si dividimos la circunferencia en m partes y que se unen los vértices de p en p , con p >1, se obtendrá un polígono estrellado de m lados si y sólo si, m y p son primos entre sí. Además, como unir los vértices de p en p es como unirlos de m–p en m – p se podrán construir polígonos estrellados considerando los números naturales menores que m/2 que sean primos con m.


