
La idea de correspondencia ha existido desde el momento que el hombre empezó a recoger datos. Mucho antes la aparición del lenguaje algebraico, en el siglo XIV el filósofo inglés del Merton College de Oxford, Th. Bradwardine (1290 – 1349), manejaba el concepto de relación variable entre diferentes cantidades representándolas mediante tablas de datos. Pero noción de función de una forma bien elaborada para ser debidamente utilizada en matemáticas apareció con la Ciencia Moderna en el siglo XVII.
A comienzos del siglo XVI lo que hoy puede parecer tan evidente como es relacionar la altura alcanzada por un proyectil disparado por un cañón con tiro oblicuo en cada punto de su trayectoria no se planteaba. N. Tartaglia (1501-1557) en su obra Nuova Scientia (1546), siguiendo la teoría aristotélica del movimiento, consideraba que la trayectoria del proyectil lanzado por un cañón tenía un tramo rectilíneo inclinado seguido de un trecho curvo y otro recto vertical; L. Collado (fl.1586-1692) Prattica manual de artillería (1586) realizó medidas de la altura alcanzada por el proyectil en diferentes puntos de su tramo de su ascenso y comprobó que su trayectoria ascendente no era rectilínea D. de Ufano (¿?-1613) recogió este dato en su Tratado de Artillería (1612).
Galileo Galilei (1564-1642) eliminó del movimiento varias cualidades, incluso observaciones visuales, y redujo la naturaleza del movimiento a términos puramente cuantitativos y medibles a los que se les podían aplicar los métodos matemáticos, como lo hizo en su obra Consideraciones y demostraciones sobre dos nuevas ciencias (1638) y demostró que el movimiento debe ser parabólico. Ver https://vicmat.com/estudio-las-trayectorias-los-proyectiles-anterioridad-galileo/
Debemos comprender las dificultades que había en esa época, a falta de buenos relojes, para medir pequeños intervalos de tiempo y cómo se las ingenió Galileo para medir el tiempo en la caída de los graves. La idea de función como relación entre variables apareció por primera vez a partir de la aparición Álgebra y la Geometría Analítica.
Newton utiliza la idea de curva y se vale de la representación geométrica, igual que lo hacían Descartes y Fermat.
Newton considera la curva continua: no considero aquí curvas construidas por partes tan pequeñas como se dese, sino descritas por un movimiento continuo. No por aposición de partes, sino por movimiento continuo de puntos son descritas y generadas las líneas; por movimiento de líneas son generadas las superficies, por movimientos de superficies los sólidos….
Parece que fue G. Leibniz (1646-1716) el primero que utilizó el término función en 1697 en una discusión con . Bernoulli para designar las cantidades cuyas variaciones están ligadas por una ley. Le decía: Para distinguir una la función de la variable x, prefiero usar la correspondiente letra mayúscula X, pues indica claramente de que variable es función; esto ayuda a la memoria. La idea no cuajó, pero L. Euler (1707-1783) acabó propuso en 1734 la notación que se maneja desde entonces, y = f(x), impuesta, sobre todo, después de la publicación de su libro Introductio in Analysin infinitorum (1748) donde define función de magnitud variable como una expresión analítica construida con esa magnitud variable y números o magnitudes constantes. (La expresión analítica de una función es una ecuación que relaciona algebraicamente las dos variables que intervienen).
L. Lagrange dio una generalización de función definiendo función de una o varias variables como cualquier expresión del cálculo Este matemático señala: «asumo que tengo un cierto número de cantidades x, y, z, y para cada valor definido de x, y, z , F tiene uno o más valores definidos correspondientes a ellos; yo digo que F es una función de x, y, z».
Debemos señalar que entre las expresiones analíticas se incluyen las series infinitas. Pero la cuestión merece un capítulo aparte.
A lo largo del siglo XVIII se entendía por función toda expresión analítica formada por la variable, constantes y funciones elementales. Además. Siguiendo la noción de curva de Newton (línea descrita por el movimiento continuo de un punto), se consideraba que las funciones eran continuas y que, además, debían tener la misma expresión formal en todo el dominio.
La definición de función parecía aceptable, pero, a medida que el Cálculo Infinitesimal se fue aplicando a diferentes problemas, aparecían nuevos matices que hacían reconsiderar la idea de que una función debía tener la misma expresión formal en todo el dominio. Los problemas surgieron en torno a las funciones arbitrarias que intervenían en las soluciones de las ecuaciones diferenciales en derivadas parciales.
J. d’Alembert (1717-1783), estudió, en 1747, el problema de la cuerda vibrante, como puede ser la cuerda de un violín. Supongamos que tenemos una cuerda elástica tensada de longitud L desde el origen de coordenadas (0,0) a otro punto (L,0) en el eje de abscisas, supongamos que tiramos de ella hasta que alcance la forma dela función y = f (z), z = x ± tv, donde f (0) = f (L) = 0 y que y = f (z) es una función continua. Si soltamos la cuerda y la dejamos oscilar libremente ¿qué formas adoptará a lo largo del tiempo?
Para el problema de la cuerda vibrante, una condición inicial natural es estirar de un punto de la cuerda, lo que da lugar a una solución que se expresa por medio de una función no derivable en un punto y con expresiones diferentes a cada lado de ese punto. Dado que se trata de una condición inicial y debía interpretarse como una función, aunque se saliera del marco de la anterior definición.

Esa función tiene una expresión diferente a cada lado de ese punto. Siendo una función que no se puede expresar con una única expresión analítica como exigía la definición de Euler.
El problema se complicó cuando Fourier (1768-1830) publicó su memoria Teoría analítica del calor (1822), donde probó que cualquier función con un número finito de discontinuidades de primera especie se podía expresar en términos de series trigonométricas. Es decir, que funciones de lo más variado admitían una única expresión analítica, lo que incluía en el concepto de función a funciones mucho más arbitrarias que las entonces admitidas. Para que existan los coeficientes de Fourier para la función basta que f(x), bastaba, según sus propias palabras: que f(x) sin nx y f(x) cos nx tuvieran área bajo su gráfica. Si f(x) es una función continua a trozos en el intervalo (0, 2pi):
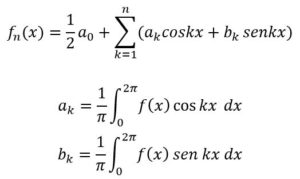
Lo que demostraba que las ordenadas no seguían una expresión analítica única y que podía tener diferentes expresiones; con lo cual había que abandonar la idea de que una función podía tener una expresión analítica única y resaltar la idea de correspondencia.
Fue P.G.L. Dirichlet (1805-1858), el que, en 1837, dio una definición que se mantiene hasta hoy día: la variable y es función de la variable x cuando a cada valor de x en un intervalo le corresponde un valor de y. Todo ello independientemente de que hubiera expresiones (una o varias) que relacionaran y con x.




