El problema que plantea es conocido en la literatura matemática como el problema de Cartas Extraviadas y fue propuesto por primera vez, de forma general, por el matemático francés P. R. de Montmort (1678-1719) en su libro Ensayo de análisis de los juegos de azar (1708) con la formulación siguiente:
Una persona ha escrito n cartas a n personas diferentes y escribió sus direcciones en n sobres. Si introdujo las cartas en los sobres al azar ¿De cuántas formas es posible que ninguna de las cartas esté dentro de su sobre correspondiente?
La demostración que vamos a exponer aquí es la realizada por L. Euler.
Las cartas se pueden colocar en los sobres de n! formas distintas. De estas n! formas diferentes aquellas en que ninguna carta está en el sobre que le corresponde la llamaremos desbarajuste y designaremos con D(n) el número de desbarajustes posibles de las n cartas
Para calcular D(n) procederemos así: Sean c1, c2, …, cn las cartas y S1, S2, …, Sn sus sobres correspondientes. Fijándonos en la posición de la carta c1 se consideran dos casos:
CASO 1. Que la carta c1 esté en el sobre S2 y la carta c2 ocupe el sobre S1. En este caso, las demás cartas c3, c4, …, cn estarán en los sobres S3, S4, …, Sn, pero cada una de esas n – 2 cartas ci no estará en el sobre correcto Si (i = 3, 4, …, n). Por lo tanto, la distribución de esas cartas será uno de los desbarajustes de esas, n-2 cartas, es decir, uno los D(n – 2) desbarajustes.
Luego si la carta c1 está en el sobre S2 y la carta c2 en el sobre S1 habrá D(n – 2) desbarajustes posibles.
CASO 2. Que la carta c1 esté en el sobre S2, pero la carta c2 no esté en el sobre S1.
En este caso la carta c1 está en el sobre S2, y hay que distribuir las cartas c2, c3, …, cn en los sobres S1, S3, …, Sn, de forma que c2 no esté en S1, c3 no esté en S3, c4 no esté en S4, así hasta la carta cn que no puede estar en Sn. Es decir, si pensamos que al no poder estar la carta c2 en el sobre S1, entonces el número de formas de realizar dicho reparto será el número de desbarajustes D(n – 1).
En resumen, estos dos casos me muestran que el número desbarajustes de n objetos en, pero, además, en los que c1 está en S2, es igual a:
D(n – 2) + D(n – 1).
Y, como un argumento similar se puede aplicar a los desbarajustes en los que c1 está en S3, S4, …, Sn, se ha demostrado que el número de permutaciones de n objetos en las que ningún objeto está en su posición original es
D(n) = (n – 1) · [D(n – 2) + D(n – 1)] (Fórmula 1)
La fórmula 1 es recursiva de segundo orden, pero puede escribirse como ecuación recursiva de primer orden con el siguiente artificio:
D(n) – n · D(n –1) = – [D(n–1) – (n–1) · D(n–2)] (Fórmula 2).
De esta fórmula se deduce, dando a n en el segundo miembro valores de n, desde n-1, n-2 … hasta 2
teniendo en cuenta que D (1) = 0 (si n = 1, con una carta y un sobre, no hay desbarajustes posibles) y D(2) = 1 (sólo hay un desbarajuste para n = 2, dos cartas y dos sobres)
Dando a n en el segundo miembro valores de n, desde n-1, n-2 … hasta 2
D(n) – n D(n – 1) = – [D(n – 1) – (n – 1) D(n – 2)] =
= (–1)2 [D(n – 2) – (n – 2) D(n – 3)] =
= (–1)3 [D(n – 3) – (n – 3) ·D(n – 4)] =
= … =
(–1)n-2 [D(2) – 2 D(1)] = (–1)n-2
Finalmente, Como (–1)n-2 = (–1)n, obtenemos la ecuación recurrente de primer orden:
D(n) – n D(n – 1) = (–1)n, (Fórmula 3)
Con D(n) = n · D(n – 1) + (–1)n y teniendo en cuenta que D(2) =1 podemos obtener D(3) = 2, D(4) = 9, D(5) = 44, D(6) = 265 y D(7) = 1854… A estos número, que son el número de desbarajustes de una permutación, se les conoce con el nombre de números de Montmort.
RELACIÓN DE LA PROBABILIDAD DE QUE UNA PERMUTACIÓN SEA DESBARAJUSTE CON EL NÚMERO e
Se trata de resolver el problema siguiente:
Problema: Una persona ha escrito n cartas a n personas distintas, escribe las direcciones de éstas en n sobres y mete al azar las n cartas en los n sobres. ¿Cuál es la probabilidad de que ninguna de las cartas esté en el sobre correcto?
Evidentemente, si son n cartas habrá n! posibilidades de ordenarlas y hay D(n) desbarajustes posibles, si Pn es la probabilidad de un desbarajuste, se tiene que:
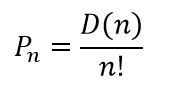
Para relacionar esta probabilidad con el número e. dividimos los dos miembros de la Fórmula 3 entre n! y se obtiene:
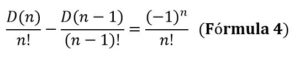
De nuevo un argumento recursivo. Damos valores de n = 2 hasta n:
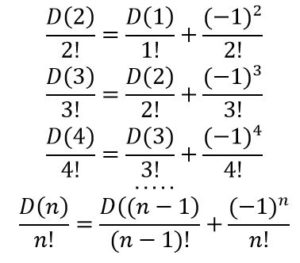
Sumando miembro a miembro y simplificando:
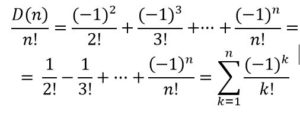
Lo que significa que la probabilidad es:
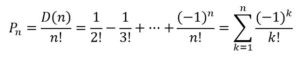
para x = – 1:
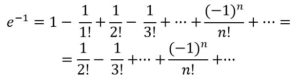
se tiene que la probabilidad Pn de que ninguna de las cartas acabe en el sobre correcto se va acercando a 1/e, que es aproximadamente 0,36788 (36,788%), a medida que n va siendo cada vez mayor, es decir:
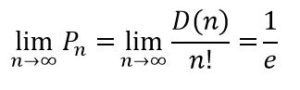
La fórmula obtenida para D(n) se puede demostrar también utilizando el principio de inclusión-exclusión, que es como lo realizó A. de Moivre (1667-1754)