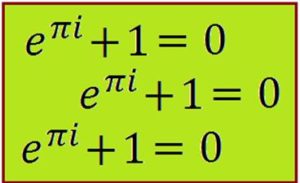
Los números complejos se descubrieron al resolver numéricamente ecuaciones algebraicas en el siglo XVI y hasta comienzos del siglo XIX no se realizó su representación geométrica que sería el punto de partida para poder dar una definición rigurosa de los mismos como pares ordenados de números reales. En este periodo de tiempo se realizaron grandes descubrimientos sobre los números complejos, su representación analítica y sus propiedades. Todos los resultados que se prdujeron en esos dos siglos salieron de la mente y del ejercicio de unos activos calculadores que, guiados por la intuición, confiaban en la generalidad de las leyes del cálculo algebraico.
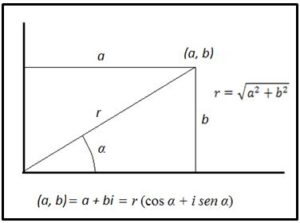
Debemos pensar que los matemáticos entre los siglos XVI y el XIX no disponían, ni concebían la representación geométrica de los complejos en el plano cartesiano, por los tanto, carecían de la representación de los números complejos que recoge en la siguiente figura y que actualmente conocen los estudiantes de secundaria. En ese tiempo solamente abordaban las investigaciones sobre números complejos con los recursos del cálculo con números reales que, además, en ese periodo se vio claramente mejorado con la aparición de los logaritmos y del cálculo infinitesimal
Cardano (1501-1576) en la edición de 1570 de Ars Magna propuso un problema en el que se manipulaban por primera vez las raíces cuadradas de números negativos. Cardano justifica la situación curiosa de un valor numérico que no tenía ningún sentido real, pero que cumplía los requisitos de ser solución del problema, que era:
Dividir el número 10 en dos partes cuyo producto sea 40.
Observó que no existía ninguna solución real, ni positiva ni negativa, que cumpliera las condiciones del problema. No obstante, el problema se podía resolver algebraicamente y confiar en el algoritmo de resolución de las mismas y planteó losiguiente: llamando x e y a las dos partes en que se divide el 10, se verificará que:
ecuación cuadrática que las soluciones:
Cardano comprobó que esos valores satisfacían las dos ecuaciones del sistema y que, por tanto, eran soluciones. Pero ¿qué significado tenían esas soluciones? Cardano consideró que eran tan sutiles que resultaban inútiles, y no especuló más sobre el tema.
R. Bombelli (1526–1572) conocía la obra de Cardano y las fórmulas de resolución de mediante radicales, de las ecuaciones de segundo, tercer y cuarto grado. Y, manipulando las soluciones de la ecuación de tercer grado, encontró las reglas fundamentales de las operaciones con los números complejos.
Bombelli observó, a simple vista, que la ecuación x3 = 15 x + 4 tenía la solución x = 4, con lo que pudo decomponerla en factores
x3 – 15 x – 4 = (x-4)( x2+4x+1) = 0
luego resolvió la ecuación de segundo grado y obtuvo las otras dos soluciones reales:
x= -2+√3 y x= -2-√3
por lo tanto, disponía de una ecuación cúbica de la que conocía sus tres soluciones reales.
Sin embargo, usando fórmula de Cardano para resolver x3 = 15 x + 4 se obtenían soluciones del tipo siguiente en las que aparecían raíces de números negativos, que carecían de sentido:
Aventuró la hipótesis de que, como los radicandos sólo se diferenciaban en un signo, con sus raíces cúbicas debía suceder lo mismo y planteó.
Calculando obtuvo: que a = 2 y b =1, con lo que obtenía que esa expresión era x = 4. Lo que mostraba una relación entre los números reales y los complejos. Y concluyó que para los las números complejos funcionaban las mismas reglas de cálculo que los números reales
Así lo recoge A. Girard (1595-1632) en su libro L’invention Nouvelle en L’algèbre (1629) en el denominó esta extensión del uso como principio de permanencia, según el cual todas las identidades algebraicas empleadas en el cálculo con números reales podían emplearse en el cálculo con números complejos. El álgebra daba más de lo que se le pedía y fue aceptado por muchos como una muestra de la generosa generalidad del álgebra.
El cálculo con números complejos se complicó cuando, a finales del siglo XVI, aparecieron los logaritmos, que se transformaron en una herramienta fundamental de cálculo, sobre todo para el uso de las tablas trigonométricas, ya que abreviaban los cálculos en astronomía y proporcionaban un método sencillo para multiplicar senos de ángulos mediante un proceso de adición directa. Desde que J. Neper (1550-1617) publicó las primeras tablas de logaritmos en su Mirifici logarithmorum canonis descriptio (1614) el descubrimiento fue bien acogido por los astrónomos, hasta el punto que fue utilizado por J. Kepler (1571-1630) para elaborar sus Tablas rudolfinas (1627).
Con los logaritmos de números complejos y de los números negativos surgieron discusiones, y desacuerdos entre grandes matemáticos. Entre 1712 y 1713, G. Leibniz (1646-1716) y J. Bernoulli (1667-1748) mantuvieron una intensa polémica epistolar sobre la existencia de los logaritmos de los números negativos y complejos.
Leibniz mantenía que log i = 0 y argumentaba de modo parecido al siguiente:
4 log i = log i 4 = log 1 = 0.
y tampoco aceptaba los logaritmos de números de números negativos.
decía que log (−2) no existe, porque si existiera, su mitad sería igual a log√(−2) , y es imposible.
Sin embargo J. Bernoulli, partía del cálculo infinitesimal y mantenía la existencia de logaritmos de números imaginarios, al relacionarlos con la trigomometría, partía de que
Pero tambiém podía calcularla por descomposición en fracciones simples
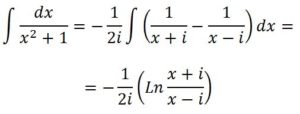
Bernoulli, integrando entre 0 y 1, proponía que, log i = iπ/2.
Hubo otra línea de trabajo con números complejos, la de los puramente calculistas, que culminaría con la fórmula de Euler que relacionaban los números complejos con la trigonometría. Debe insistirse en que estas esta relaciones se lograron sin disponer de una representación geométrica de los números complejos y es sorprendente, que disponiendo de estas fórmulas, no repararan en la versión geométrica de tal representación.
El matemático inglés R. Cotes (1682-1716) descubrió en 1714 la relación entre las funciones trigonométricas y el logaritmo de las mismas, i x = ln ( cos x + i sen x ) que era la expresión logarítmica de la fórmula de Euler eix = cos x + i sen x. La fórmula fue publicada en su obra póstuma Harmonia mensurarum (1722).
A. De Moivre (1667-1754) es recordado por una fórmula que nunca escribió explícitamente, sino que en una nota publicada en 1722, afirmaba que podía obtener una relación entre x y t (que representaban los senoversos de dos ángulos (senver x = 1-cos x) que estaban en la razón 1 a n) eliminando z de las dos ecuaciones siguientes:
1– 2zn + z2n = -2znt y 1 – 2z + z2 = –2zx
En este resultado está implícita la fórmula de Moivre (Morris Kline, El pensamiento matemático… p. 545) que es: (cos x + i sin x ) n = cos nx + i sin nx
Euler (1703-1783) desarrolló la fórmula utilizando la función exponencial en vez del logaritmo y lo comunicó en una carta enviada a Ch. Goldbach (1690-1764) en 1741, pero la publicó en su obra Introductio in analysin infinitorum en 1748. La “demostración” la realizó a partir de los desarrollos en serie de la función exponencial, del seno y del coseno:
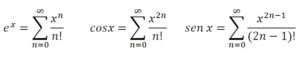
Sustituyendo en el desarrollo de la exponencial x por ix se obtiene:
Es decir, ei x = cos x + i sen x
Aunque la fórmula es correcta, el método que utilizó Euler para obtenerla no constituye una demostración, debido a que el desarrollo en serie de ex fue deducido suponiendo que x era una variable real y la sustitución de x por ix requiere una justificación basada en la teoría teoría de funciones de variable compleja. Pero no era el momento, en este periodo de la historia de los números complejos aún se funcionaba con el principio de permanencia de Girard. El cálculo se había aplicado con éxito a la física y los resultados justificaban los métodos utilizados.
De esta fórmula de Euler concluye que ese puede deducir que el logaritmo de -1 no es un número real, sino imaginario, pues para x = π, eiπ =-1, y, por tanto, ln (-1) = iπ.
Euler había obtenido una de las formulas mas hermosas de las matemáticas, pero aún seguía pensando:
Como todos los números imaginables son mayores, menores o iguales a cero, entonces es evidente que la raíz cuadrada de un numero negativo no puede ser uno de estos números,[…] y esta circunstancia nos lleva a que tales números, por su naturaleza son imposibles y normalmente son llamados imaginarios o números falsos, porque solo existen en la imaginación.
Es interesante notar que ninguno de estos protagonistas vislumbrara la interpretación geométrica de los números complejos señalada anteriormente. La representación de los números complejos como puntos en el plano cartesiano apareció en 1787 la propuso el matemático noruego-danés Caspar Wessel (1745-1818) y francés Jean-Robert Argand (1766-1822) pronto aceptada.
