El factorial de un número entero positivo n es una expresión que se calcula multiplicando n por los números enteros positivos menores que el. Se designa con n!
Es decir, n! = n·(n-1)·(n-2)···3·2·1
El factorial se emplea con profusión en combinatoria. El significado del factorial de n es el número de reordenaciones que se pueden hacer con n elementos diferentes y tiene una generalización que extiende el factorial al cuerpo de los números reales y al cuerpo de los números complejos mediante la función gamma, que cumple que Γ(n+1) = n!
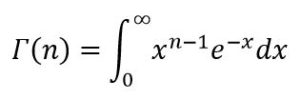
El descubrimento de la función Ganma se debe a L. Euler (1707-1783), por la cual a veces se suele decir que es una integral euleriana. A continuación muestran una serie de problemas relacionados con factoriales:
PRIMERO: ¿En cuántos ceros acaba 20!?
Solución: Si acaba en un cero será divisible entre 10 = 2×5. Por tanto, acabará en tantos ceros como parejas de doses y cincos tenga la descomposición en factores primos de 20!. En realidad habrá tantos ceros como cincos tenga la descomposición, que son 4.
20! = 1·2·3·(2·2)·5·(2·3)·7·(2·2·2)· ··· ·(2·5)· ··· ·(3·5)· ··· ·(2·2·5) =…
Tiene cuatro factores primos 5, que son aportan los factores 5, 10.15 y 20
20! = 2.432902.008176.640000
SEGUNDO: ¿Cuál es la máxima potencia de tres por la que es divisible 20!?
Solución:
Los factores del factorial que son múltiplos de tres son: 3, 6, 9, 12, 15, 18. Los factores 3, 6, 12 y 15 tienen un factor primo tres; los fatores 9 y 18 tiene dos factores tres cada uno, en total hay ocho factores tres, luego la máxima potencia de tres que divide l factorial será: 38
20! = 1·3·2·2·5·2·3·7·23· 32·2·5·11·22x3·13·2·7·3·5·24·17·2·32·19·22x5 =
= 218·38·54 ·72·11·13·17·19
La máxima potencia de tres en 20! es 8
TERCERO: ¿Cuantos divisores tiene 20!?
Solución: La descomposición en factores primos de 20!:
20! = 218 ·38 ·54 ·72 ·11·13·17·19
El número de divisores será el producto de los exponentes de su descomposición factorial incrementados en una unidad, es decir : 19·9·5·3·16= 41.040
RESULTADO IMPORTANTE: Si N tiene una cifra Log N = 0,abc…, (parte entera 0); Si N tiene dos cifras Log N = 1,abc… (parte entera 1). Si N tiene tres cifras Log N = 2,abc… (parte entera 2). Si N tiene n+1 cifras Log N = n,abc… (parte entera n). Luego aplicaremos la regla siguiente:
Número de cifras de N = 1+ Ent (Log N)
CUARTO: ¿Cuántas cifras tiene el número 235 x 538 ?
Solución. 235 x 538 = 53·235· 535 = 53·1035 = 125· 1035, es decir 125 seguido de treinta y cinco ceros, por tanto, 38 cifras.
Aplicando la regla anterior procederemos así: Si N = 235 x 538
Log N = 35 log 2 +38 log 5 =10, 5360 + 26,5609 = 37, 0969
Número de cifras de N = 1+ Ent (Log N) = 1 + Ent (37, 0969) =1 +37 =38
QUINTO: ¿Cuántas cifras tiene el número 7125?
Solución: Si N = 7125
Aplicando la fórmula del resultado importante anterior:
El número de cifras de N = 1 + Ent (Log N) =1+ Ent (125·lg7) =106
SEXTO: ¿Cuantas cifras tiene nn?
Solucion: Si N = nn Número de cifras de N = 1+ Ent (n·Log n)
Si N = 1010, entonces: Nº de cifras de N = 1+ Ent (10·Log 10) = 1+ 10 = 11
Si N = 100100, entonces: Nº de cifras de N = 1+ Ent (100·Log 100) = 1+ 200 = 201
Si N = 10001000, entonces: Nº de cifras de N = 1+ Ent (1000·Log 1000) = 1+ 3000 = 3001 cifras
Y así sucesivamente:
1000010000 tiene 40.001 cifras
100.000100.000 tiene 500.001
1.000.0001.000.000 tiene 6.000.001
SÉPTIMO: ¿Cuántas cifras tiene 40! ?
Solución: Veremos que tiene 48. Ya que el número de cifras es:
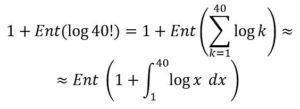
Calculemos el paréntesis:

Luego 40! tiene 48 cifras.
40! = 815915.283247.897734.345611.269596.115894.272000.000000