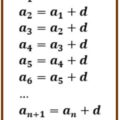
En febrero de 1975, Steve Selvin (n.1941) publicó en la revista trimestral The American Statistician una carta titulada Un problema de probabilidad, en ella planteó y resolvió un problema, que conocemos como el Problema de Monty Hall. La carta levantó algunas críticas tanto por la solución aportada por Selvin como por lo sorprendente de su resultado. Seis meses después apareció en la misma revista una carta de seguimiento del autor titulada Sobre el problema de Monty Hall. En esta carta, Selvin expuso una solución basada en el teorema de Bayes y explicó algunos detalles sobre el comportamiento del moderador del concurso.
El problema permaneció dormido hasta que alcanzó una enorme difusión cuando Marilyn vos Savant lo publicó en su columna de la revista Parade en 1990. Parade es una revista que se vende cada domingo como suplemento buena parte de los periódicos en los Estados Unidos. Con este medio de difusión, el problema el problema de Monty Hall se y dio a conocer en todo el mundo, se publicaron bastantes artículos, se convirtió en un problema popular y aparece en muchos libros de texto de introducción a la probabilidad y estadística.
El problema se puede plantear así:
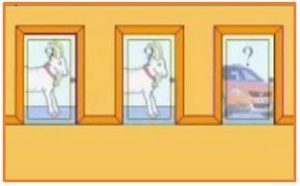
Supongamos un concurso el presentador ofrece al concursante la posibilidad de elegir entre tres puertas. Detrás de una de ellas hay un coche, y detrás de las otras, cabras. El concursante elige una puerta, por ejemplo, la nº 1, y el presentador, que sabe lo que hay detrás de las puertas, abre otra, por ejemplo, la nº 3, y descubre una cabra. Entonces el presentador pregunta al concursante: ¿prefieres escoger la nº 2?.
La pregunta que se plantea es si el cambio de elección aumenta la probabilidad de ganar, es decir, de conseguir el coche, el cambio de elección.
El planteamiento inmovilista es mantenerse en la elección primera:
El concursante elige una de las tres puertas, evidentemente la probabilidad de ganar (conseguir el coche) será 1/3. Cuando el presentador le diga si quiere elegir de nuevo, y cambiar su elección primera, piensa: A lo mejor ya he elegido el coche y, si no lo he elegido, el coche estará tras una de las dos puertas y puedo acertar o fallar con igual probabilidad (1/2) y para eso, no cambio.
En este caso, cuando no cambia su primera elección, la probabilidad de ganar el coche se mantiene en 1/3.
Si el concursante cambia su elección aumentan sus probabilidades de ganar:
Analizaremos las dos posibilidades:
- Si en la primera elección ha elegido la puerta con coche (Prob = 1/3), cuando el presentador le dice que cambie, sabemos que le abrirá la puerta que contiene una cabra, cambia y perderá siempre, entonces probabilidad de ganar es 0.
- Si en la primera elección ha elegido la puerta con cabra (Prob = 2/3), cuando el presentador le dice que cambie sabemos (y eso es lo importante) que le abrirá la puerta que contiene la otra cabra, (si le abre la del coche la elección no sería dudosa) entonces el coche está necesariamente en la otra, el concursante cambia y gana con probabilidad 1. Entonces probabilidad de ganar es 2/3.
Esto se podría expresar, usando el teorema de Bayes:
A = {Elegir coche en la primera opción} =1/3 y
Ac = {Elegir cabra en la primera opción} = 2/3
B = {Elegir el coche en segunda opción}
P(B) = P(BႶA) + P(BႶAc) =
= P(B|A)·P(A) + P(B|Ac)·P(Ac) =
= 0·(1/3) + 1·(2/3) = 2/3
Luego conviene cambiar siempre la primera elección porque duplica la probabilidad de ganar