Existen algunos, Rey Gelon, que creen que el número de granos de arena es infinito en multitud. Arquímedes
Cuando tratamos de contar un conjunto o una colectividad rara vez podemos ordenas sus elementos y comenzar a contar, 1, 2, 3… hasta el final. Por ejemplo, para contar el número de participantes en una manifestación el procedimiento consiste en medir la distancia desde la cabecera hasta el final del recorrido. A continuación se calcula el área útil que ocupan las personas descontando la superficie ocupada por vehículos, los huecos entre grupos de manifestantes, etc. Cuando la densidad de manifestantes es muy grande se estima un máximo de cuatro personas por metro cuadrado, mientras que en otras zonas menos densas se cuentan de una a dos personas por metro cuadrado. Cuando los manifestantes caminan se suele estimar la densidad de un manifestante por metro cuadrado.
También se pueden calcular aproximadamente de forma indirecta el número de granos de arroz que puede haber en un kilo. Basta con tomar una muestra de 100 granos de arroz que pesa P (P ≈ 2,69 gramos). El número de granos se calcula de forma sencilla 100·(1000/P). Luego habrá aproximadamente 37.175 granos de arroz en un kilo.
Los métodos estadísticos nos permiten evaluar el número de peces que hay en un lago. Supongamos en el lago hay N peces. Tomamos una muestra de M peces y los marcamos con el fin de poderlos reconocer. y los devolvemos al agua. Pasado un tiempo, tomamos otra muestra de tamaño M’ y contamos los peces marcados que son C y se tiene la siguiente proporción:
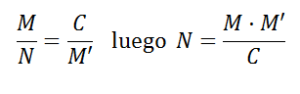es la población estimada de peces en el lago.
Más laborioso y difícil resultó contar el número de moléculas contenidas un volumen determinado de gas en condiciones normales (a una atmósfera y a 0ºC). Las moléculas de los gases no se veían a simple vista y, además, estaban en continuo movimiento, pero había una serie de indicios para creer que los átomos y las moléculas existían sin necesidad de un microscopio que las mostrara como los aportados por J. Dalton (1766-1844).
Dalton había observado en 1805 que los elementos que intervenían en las reacciones químicas guardaban entre si relaciones sencillas de de peso y formuló la hipótesis de que esas relaciones tan sencillas en las reacciones químicas se debían a que la materia estaba formada por partículas pequeñas e iguales que se unían entre sí en la misma proporción dando lugar macroscópicamente a esas relaciones entre los pesos. Dalton expuso su teoría en 1805 y en su obra Nuevo sistema de filosofía química. Combinando hidrógeno y oxígeno y encendiéndolos con una chispa, se producía agua con un ruido .Y observó que para producir dos moléculas de agua (H2O) debían reaccionar dos moléculas de hidrógeno (H2) con una molécula de oxígeno (O2), según se indica en la reacción:
2H2 + O2 = 2H2O + Energía
J.L. Gay-Lussac (1778-1850) experimentó con gases y observó que las relaciones volumétricas en las reacciones químicas guardaban entre si razones tan simples como, 1:2, 1:3, 2:3, etc., También después constató que, una vez acabada la reacción, se producía una reducción de volumen y que la relación entre los volúmenes de los gases componentes y del gas resultante se expresaba con número entero. Como se podía observar en la producción de agua.
En 1811, A. Avogadro (1776-1856) y A. M. Ampère (1775-1836) interpretaron la experiencia de Gay-Lussac en términos de teoría atómica y formularon la hipótesis que hoy conocemos como hipótesis de Avogadro, que decía el número de moléculas en un volumen de gas era el mismo para todos los gases, si éstos están a igual presión y temperatura.
La hipótesis de Avogadro colocaba a la química y a la física ante varios problemas: calcular cuántas moléculas por unidad de volumen había en un volumen determinado de gas, cuál era el tamaño de las moléculas y a qué velocidad movían. Estas cuestiones interesaban a los científicos, porque relacionaban a la química con la naciente termodinámica, ya que teoría atómica de la materia relacionaba el calor que se producía en el rozamiento de dos cuerpos con el movimiento de las partículas que los formaban y conectaba la temperatura con la energía media de las moléculas que la componen.
El proceso de contar las moléculas de una gas fue complicado y se emplearon grandes científicos que aportaron brillantes ideas. A continuación se esbozan las ideas ylo procesos más destacables del delicado proceso que se siguió:
1.– La primera suposición fue que las moléculas se comportaban como partículas esféricas y que los choques y los recorridos de las mismas seguían las leyes de la mecánica newtoniana.
2.– R. Clausius (1822-1888) dedujo que las moléculas de un gas tenían un recorrido medio L que era inversamente proporcional a n·D2 y obtuvo la fórmula:
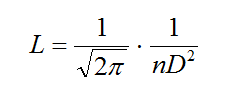donde n era el número de moléculas y D diámetro medio de las mismas. La fórmula decía que el recorrido medio de cada molécula era inversamente proporcional al númenro de molécuals n y a su sección D2. Pero ni n ni D eran valores conocidos.
3.– J. C. Maxwell (1831- 1879) probó que el coeficiente de viscosidad (η) de cualquier gas se podía medir experimentalmente y se podía expresar en función del recorrido libre medio (L) y la velocidad media de agitación de las moléculas (v) y la densidad del gas por la fórmula (ρ): η = ρ· ν· L.
4.– Por otra parte, la velocidad media con la que se movían las moléculas del gas a una temperatura T se podía calcular mediante la fórmula:
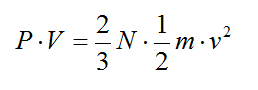Donde P es la presión, V el volumen del gas, N es el número de moléculas y v es la velocidad media de las moléculas, m es la masa de cada molécula. De esta fórmula, y de la ecuación de los gases perfectos P·V = RT, se llega a que
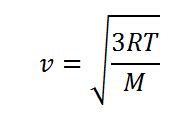Resultó que la velocidad media a la que se movían las partículas se podía calcular y era la asombrosa velocidad v = 461 m/s y con ella y con la fórmula obtenida por Maxwell η = ρ· v· L se pudo calcular el recorrido libre medio L y con él, el tiempo medio entre dos choques sucesivos que resultó ser de 10-10 segundos aproximadamente. Teniendo en cuenta la ecuación de Clausius con la velocidad se podía conocer L y con él calcular el valor del producto nD2. Conocido el prodicto nD2 ya sólo faltaba conocer una relación entre n y D. para poder calcular estosvalores.
5.– La idea para hallar una nueva una relación entre n y D, se le ocurrió en 1865, al físico austriaco J.J. Loschmidt (1821-1895), que reparó en la idea de que las moléculas de un gas no dejaban espacio entre ellas cuando se el gas se licuaba. Las moléculas del gas licuado estarían en contacto unas con otras como sucedía en un recipiente lleno de canicas y el volumen total del gas licuado será V = nD2. Teniendo en cuenta la simetría de los posibles empaquetamientos de las esferas, Loschmidt llegó a la conclusión de que el diámetro de las moléculas era del orden de D = 10-8 cm = 1 angström y de que el número de moléculas n en un mol debía estar comprendido entre 1023 y 1024. Actualmente se estima el número de Avogadro en 6,028·1023.
Con este proceso se consiguieron contar las moléculas de un volumen de un gas dado, que en un mol de gas 22, 4 litros a 1 at. y 0ºC había 6,028·1023
