La media aritmética y la media geométrica pueden ser utilizadas para resolver problemas de optimización. En algunos casos, como en el Problema 4, con su ayuda, se resuelve el problema de isoperimétricos para triángulos de una forma rápida y elegante.
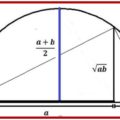
La media aritmética de dos números positivos a y b es mayor o igual que su media geométrica y sólo son iguales ambas medias cuando a = b. Es decir:
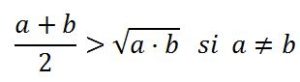
y ambas son iguales si a = b.
Esto quiere decir que la media geométrica está siempre acotada superiormente por la media aritmética. Esta propiedades la podemos expresar simplemente en forma de suma y productos de números de la siguiente forma:
Si a y b son dos números positivos tales que S = a + b y P = a·b
De la identidad 4a·b = (a + b)2 – (a – b)2 se deduce que 4 P = S2 – (a – b)2
Por lo tanto: entre todos los pares de números a y b cuya suma sea S, el producto P de esos números sera máximo cuando ambos sean iguales, es decir, cuando a = b, ya que (a – b)2 > 0. Es decir, P será máximo cuando se cumpla que:
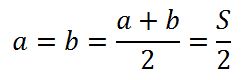
Resultado también es cierto para es cierto cuando tenemos más sumandos, es decir, Entre todos los números x1, x2, … xn cuya suma es S = x1 + x2+ … + xn , el producto esos números: P = x1 · x2· … · xn será máximo cuando todos los sumandos sean iguales:
![]()
Sin ánimo de dar una demostración rigurosa se puede intuir fácilmente que es cierta, ya que si, por ejemplo, x1 y x2 son dos factores desiguales, sustituyéndolos ambos por su media aritmética, es decir respectivamente por
![]()
el producto aumenta, mientras que la suma permanece constante, por lo tanto, mientras el producto contenga factores desiguales puede ser aumentado sin alterar la suma de los factores y, en consecuencia, se puede intuir que el producto será máximo cuando todos los factores sean iguales.
Consecuencias y problemas:
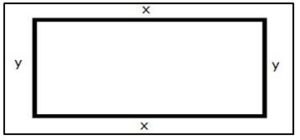
1- Problema 1.- Entre todos los rectángulos de perímetro 20m, ¿Cuál es el que tiene mayor área?
Solución: Los rectángulos de dimensiones x, y deben cumplir que, 2x + 2y = 20 o, equivalentemente, que x + y = 10. Como queremos que x · y sea máximo. De la consecuencia b) anterior: Para que dos cantidades tales que su suma es constante x + y = 10, para que su producto sea máximo se debe cumplir que . Por lo tanto, se cumple que x = y = 5. Por lo que el rectángulo de área máxima será el cuadrado de lado 5m.
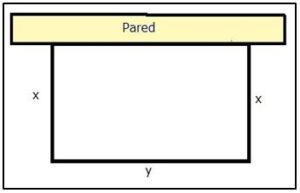
2.- Problema 2.- Disponemos de 200m de cerca con la que se quiere hacer un vallado rectangular aprovechando una pared ¿Cuáles deben ser las dimensiones para que la superficie cercada sea máxima?
Solución: Según la figura con 200m de valla se debe cumplir que 2x + y = 200, haciendo 2x = a, la expresaremos en la forma a + y = 200. Deseamos que la superficie encerrada sea maxima, es decir, que el producto x · y sea máximo o, lo que es igual, queremos que los productos:
a/2 ·y = (1/2) a · y, que significa que a·y sea máximo
con la condición que a + y = 200, lo que se cumplirá cuando a = y. Luego: y + y = 200 ⇒ y =100 m, a = 100m y x = 50m
3.- Problema 3.- ¿Qué valor tiene que tomar x para que el producto (a – x)2·(a + x)3 tome el valor máximo?
Respuesta: Llamemos f(x) = (a – x)2·(a + x)3. La suma de los cinco factores es
2(a – x) + 3(a + x) = 2a – 2x + 3a +3x = 5a + x,
que depende de x y, poe tanto, no es constante y no se puede aplicar la regla de que el producto ha de ser máximo cuando los factores sean iguales. Transformamos la función f(x) en otra g(x) que tome el valor máximo para el mismo valor de x y que cumpla que la suma de sus factores sea constante. La función será k·f(x) con k = 2-2·3-3. La nueva función será:
![]()
La suma de los cinco factores de g(x) será constante como se ve a continuación:
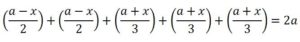
El máximo lo alcanzará cuando los sumandos sean iguales, es decir:
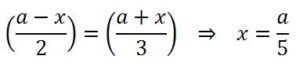
4.- Problema 4.- Demostrar que el triángulo equilátero es el triángulo de mayor área entre todos los que tienen igual perímetro.
Respuesta: La fórmula de Herón para calcular el área, A, de un triángulo cuyos lados miden a, b y c permite calcular el área en función de sus lados:
![]()
donde p = (a + b + c)/2, esto es, el semiperímetro del triángulo.
Maximizar A equivale a maximizar A2 = p (p − a) (p − b) (p − c), lo que equivale, a su vez, (puesto que p es constante) a maximizar el producto P = (p − a) (p − b) (p − c). Como la suma de los factores de ese producto es constante ya que: (p − a) + (p − b) + (p − c) = p
Entonces , A 2, será máxima cuando sea máximo el producto P = (p−a) (p−b) (p−c), el cual será máximo cuando los tres factores son iguales:
p − a = p − b = p − c ⇒ a = b = c.
Por tanto, el triángulo es de mayor área entre todos los que tienen igual perímetro es el equilátero.