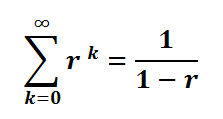En la matemática griega la rama dominante era la Geometría, representada en los Elementos de Euclides. La Aritmética se servía de la solidez de las construcciones geométricas para hacer razonamientos, deducciones e incluso operaciones numéricas. En el siglo I Nicómaco de Gerasa (60-120) escribió una Aritmética en la que prescindía de la representación geométrica de Euclides, pero aceptaba la superstición pitagórica de las propiedades místicas de los números.
Nicómaco separó el concepto de número de la noción de magnitud geométrica y definió número como conjunto finito de unidades. Además, clasificó los números según distintos criterios: había números pares e impares; primos y compuestos; superabundantes, perfectos y deficientes; triangulares, cuadrados, pentagonales…; piramidales, cubos, etc.
Pero en este trabajo destacaremos, por su carácter visual e intuitivo, los métodos utilizados para calcular sumas de sucesiones de números por métodos geométricos en los que la semejanza y las simetrías observadas en las representaciones geométricas de los números, jugaban el mismo papel que el principio de inducción matemática en aritmética.
1.- Suma de n enteros consecutivos: Comenzaremos con un caso particular, calcular la suma de los cinco primeros enteros: 1 + 2 + 3 + 4 + 5. Para ello en un rectángulo 5×6 observamos que la suma es la mitad de área del rectángulo, es decir, 15.
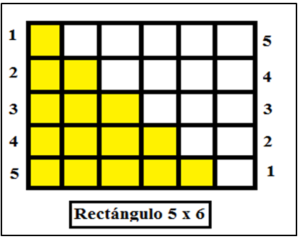
Para calcular 1 + 2 + 3 +···+ n se utilizará un rectángulo de dimensiones n·(n+1) se puede observar que:
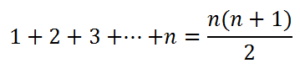
2.– Suma de una progresión aritmética: Como en el caso anterior se comenzaremos por calcular un caso particular: sumar los siete términos de la progresión aritmética de razón tres: 2 + 5 + 8 + 11 + 14 + 17 + 20.
Para ello, en un rectángulo cuya base es la suma del primer y del último término y la altura es el número de términos que deseamos sumar, observamos que la suma de los siete términos (representada en amarillo) es la mitad de área del rectángulo, es decir, 77.
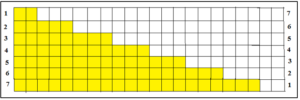
Para sumar a1 + a2 + a3+ ··· + an, en un rectángulo de dimensiones n·( a1 + a2) se puede observar que:

3.- Suma de los n primeros números impares: Calcularemos en primer lugar la suma de los siete primeros números impares: 1 + 3 + 5 + 7 + 9 + 11 + 13, para hacer el cálculo geométricamente lo dispondremos se indica en la figura observando que:

1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16
1 + 3 +5 + 7 + 9 = 25 1 + 3 + 5 + 7 + 9 + 11 = 36 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49
Para sumar los k primeros números impares hay que tener en cuenta que el número impar n que ocupa el lugar k es n = 2k-1 y la suma:
1 + 3 + 5 + ··· + 2k-1 = k2.
Así, la suma de los números impares del 1 al 2017 será, teniendo en cuenta que :
2017 = 2·1008 – 1 k2 = 10082 = 1.014.049
4.– Suma de la progresión geométrica: 1 + r + r2 + r3 + r4 +…+ r n… r <1
Esta es una suma infinita de términos menores que uno (salvo el primero). Para determinarla partiremos del cuadrado de lado unidad ABCD. Sobre el lado CD tomamos una distancia CE = r, que es lado de un nuevo cuadrado. Sobre él adosamos un cuadrado de lado C’E’ =r2. Los puntos A, E, E’, E’’… están alineados y la recta que los une corta a la prolongación del lado BC del cuadrado inicial en el punto F, según se observa en la figura
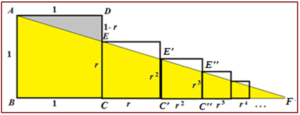
Los triángulos ABF y ADE son semejantes, por lo tanto se cumple la relación:

O, en lenguaje más compacto: