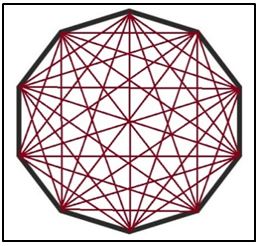
Si dividimos una circunferencia en n partes iguales por n puntos y unimos los puntos sucesivamente obtenemos un polígono regular de n lados. Con este punto de partida podemos plantearnos una serie de cuestiones.
En primer lugar una de combinatoria
PRIMERA. ¿Cuántas diagonales tiene polígono regular de n lados?
Solución: La diagonal es la línea que une dos vértices no consecutivos del polígono (Si une dos consecutivos sería lado del polígono), por lo tanto, el número de diagonales será: Las combinaciones posibles de dos vértices menos el número de lados:
C n,2 – n = n(n – 1)/2 – n = (n2-3n)/2 = n(n-3)/2
SEGUNDA. En un polígono regular de un número impar de vértices de cuántas manera podemos seleccionar tres de ellos para que uniéndolos mediante segmentos rectilíneos se forme un triángulo rectángulo
Solución: Para que el triángulo sea rectángulo la diagonal del polígono regular que sea la hipotenusa del triángulo rectángulo debe pasar por el centro de la circunferencia circunscrita, pero como el número de vértices es impar ninguna pasará por el centro y no se formará ningún triángulo rectángulo.
Algo diferente pasa cuando el polígono regular tiene un número par de vértices:
TERCERA.- En un polígono regular de un número par de vértices, A1, A2,…, A2n-1, A2n, se unen tres de ellos mediante segmentos rectilíneos y se forma un triángulo Ai, Aj, Ak . Calcular de cuántas formas podemos elegirlos para que:
a) Formen un triángulo rectángulo b) Formen un triángulo obtusángulo
c) Formen un triángulo acutángulo
Solución: En primer lugar determinaremos el número total de triángulos que se pueden formar con los con los A1, A2,…, A2n-1, A2n puntos que será el número de total de tríos posibles que se pueden formar con ellos, serán C2n, 3 ,
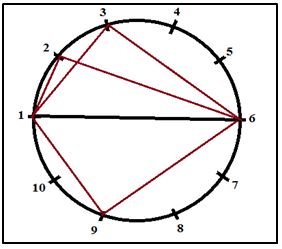
a) Para que un trío de estos puntos determine un triángulo rectángulo dos vértices tienen que ser extremos de un diámetro. Si trasladamos uno de los vértices seleccionados que forme ángulo agudo hasta el punto A1, el otro vértice de ángulo agudo estará en el punto diametralmente opuesto: An+1, El vértice del ángulo recto ocupará cualquiera de los A2, A2,…, An o An+2, …, A2n Es decir, cualquiera de las 2n-2 posiciones y como hay n posiciones diametrales de los ángulos agudos el número de tríos Ai, Aj, Ak que forman triángulo rectángulo será:
Triángulos Rec = n(2n-2) = 2n(n-1)
b) Para que las ternas Ai, Aj, Ak formen un triángulo obtusángulo: Sabemos que cualquier triángulo obtusángulo va a dejar el centro de la circunferencia, O, fuera de él. Por lo que si lo giramos en sentido directo, o inverso, alrededor de O, podemos conseguir que uno de los vértices agudos esté en A1. Los otros dos ángulos estarán en el conjunto {A2,A3, . . . , An }, ó bien en {An+2, An+3, . . . , A2n}, luego habrá 2C n-1, 2. Como puede trasladarse a A1 un vértice agudo del triángulo, habrá: 2n [2·C n-1, 2 ] y como cada triángulo lo hemos contado 2 veces, uno para cada vértice agudo, el número de triángulos obtusángulo será [2n·C n-1, 2 ]
Triángulos ob = [2n·C n-1, 2 ] = n(n-1)(n-2)
c) Los que forman un triángulo acutángulo:
Triángulos Acu = Nº total de triángulo – Triángulos Rec – Triángulos Ob =
= C 2n, 3 – 2n(n-1) – n(n-1)(n-2) =
= C 2n, 3 – 2n(n-1) – n(n-1)(n-2) =
C 2n, 3 – 2n(n-1) [2+(n-2)] = C 2n, 3 – 2n2(n-1) =
