EFECTO DOPPLER EN LAS FRECUENCIAS DE LAS NOTAS MUSICALES

El efecto Doppler fue descubierto en 1842 por Christian Doppler (1803-1853) en una memoria  titulada Sobre la luz coloreada de las estrellas binarias. La Memoria fue presentada en la Royal Bohemian Society of Sciences, centro científico más importante de las tierras de la Corona de Bohemia y que actualmente se conoce como Academia Checa de Ciencias.

En el documento demostraba matemáticamente como la frecuencia del sonido emitido por una fuente en movimiento variaba para un observador estacionario y pasaba a especular que el color de la luz de una estrella debería alterarse de acuerdo con la velocidad con que se alejara de la Tierra. Este principio pronto fue conocido como el efecto Doppler. El efecto Doppler se ha utilizado para apoyar la Teoría del Big Bang.

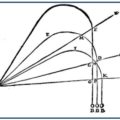
Doppler, estudiando este fenómeno con el sonido, se preguntó por qué razón el sonido se percibía  de modo distinto, según la fuente se alejara o se acercara al receptor. Se sabía que el sonido se transmitía por una serie de ondas que se desplazaban en un medio determinado, y el físico estudió el ejemplo siguiente: cuando una locomotora se acercaba al punto donde estaba situado un observador, cada onda sonora sucesiva se percibía casi superpuesta a la anterior (un sonido agudo), de modo que el oído la captaba con frecuencia creciente; por el contrario, al alejarse, la frecuencia captaba con frecuencia decreciente, las ondas se espaciaban cada vez más, la frecuencia era menor (un sonido grave).

En junio de 1845 un meteorólogo de Utrech, Christoph H.D.Ballot (1817-1890), realizó un experimento del efecto Doppler durante en el trayecto en tren de Utrech a Amsterdam. Doppler realizó un experimento poco después. El experimento consistió en hacer  que una locomotora llevara acercara un vagón cargado de músicos hacia el punto de observación emitiendo todos la misma nota musical y luego se alejara de él, a diferentes velocidades. En el punto de observación otros de músicos de fino oído se ocupaban de registrar los cambios de frecuencia que se producían en un diapasón en las diferentes idas y venidas del tren.

Debemos recordar que la locomotora Rocket de Stephenson en 1830 era de al menos 48 km/h y que en 1848, los pasajeros podían viajar de Londres a Glasgow en 12 horas, con trenes que alcanzaban velocidades próximas 80 km/h.

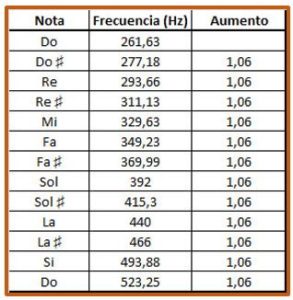
Para describir el experimento del efecto Doppler de Ballot consideramos las frecuencias de las notas musicales en herzios recogidas en la siguiente tabla (recordaremos que un herzio significa un ciclo por segundo, entendiendo ciclo la repetición de un suceso. Por tanto, el hercio es el número de veces por  segundo que se repite una onda).

Para describirlo matemáticamente consideremos un foco que emite ondas con una frecuencia f₀, las cuales se desplazan a una velocidad v. Para dar una expresión matemática al efecto Doppler razonaremos así:

1. En un periodo de tiempo ∆t el foco emite un número de ondas N = f₀∆t
2. El primer frente de ondas se habrá desplazado una distancia d = v∆t
3. Si el foco se desplaza hacia un observador a una velocidad u_s y se habrá desplazado una distancia d’= u_s∆t
4. En el sentido del avance del foco las N ondas emitidas en el tiempo ∆t están contenidas en el intervalo d – d’. Por tanto: d – d’ = v∆t – u_s·∆t = (v – u_s)·∆t
5. Pero en d – d’ caben N ondas, por tanto, la longitud de onda será en el sentido del avance:

λ_a = (d – d’) / N = [(v – u_s)·∆t] / [f₀·∆t ] = (v – u_s) / f₀  =

1. En el sentido contrario al avance del foco las N ondas emitidas en el tiempo ∆t están dentro del intervalo d + d’. Por tanto: d + d’ = v∆t + u_s·∆t = (v + u_s)·∆
2. Pero en d ´+ d’ caben N ondas, por tanto, la longitud de onda será en el sentido contrario al avance será:

λ_b = (d + d’) / N = [(v + u_s)·∆t] / [f₀·∆t ] = (v + u_s) / f₀  =

Resumiendo, la frecuencia f_a en el sentido del avance será:

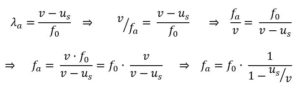
Con un razonamiento análogo, la frecuencia f_b en el sentido contrario al avance será:

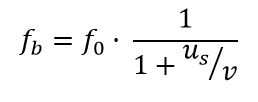Observación:

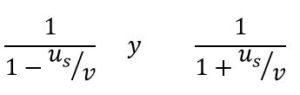
Son los factores en los que aumenta o disminuye la frecuencia de una señal que emite a una velocidad v y cuyo foco emisor se desplaza  a una velocidad u_s.

Ejemplo: Un violinista da la nota La de 440 Hz mientras se desplaza hacia un observador a una velocidad de 50 Km/h (13,8 m/s.) ¿Qué nota percibirá observador?

Una nota con frecuencia, f_a = 457,6 Hz

Ejemplo: Un violinista da la nota La de 293,66 Hz mientras se desplaza hacia un observador a una velocidad de 75 Km/h. (20,83 m/s.) ¿Qué nota percibirá observador?

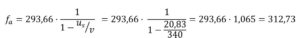
Una nota con frecuencia,  f_a = 312,75 Hz (Re#)

Nota: Se puede admirar el oído de los músicos del experimento de Ch. H.D.Ballot para poder apreciar la variación del tono de la nota emitida por los músicos del tren mezclado con el sonido de la locomotora