Los problemas que se recogen en este trabajo parten del problema conocido como problema de los círculos de Malfatti.
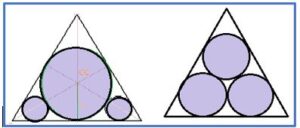
Gianfrancesco Malfatti (1731 –1807) fue un matemático italiano relacionado con la ilustración y el enciclopedismo. El enunciado del problema de Malfatti, en términos generales, consiste en encontrar tres círculos, dentro de un triángulo cualquiera, que sean tangentes entre sí y tangentes a dos lados del triángulo. Malfatti pensaba que, entre todos los tríos de círculos que cabían en un triángulo sin solaparse, los suyos cumplían la condición de sumar la mayor área posible.
En suma, el problema de encontrar la solución que maximiza la suma de la superficie total de los tres círculos es diferente al de encontrar los círculos de Malfatti.
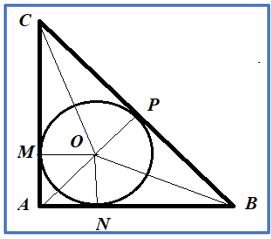
PROBLEMA 1.- Calcula el radio del círculo inscrito en un triángulo rectángulo isósceles en el que sus catetos miden 4 cm.
Respuesta:
Las bisectrices de los tres ángulos se cortan el incentro, que es el punto O. Este punto equidista de los lados del triángulo y OM = ON = OP = r
Se cumple que:
Área (ABC) = Área (OBC) + Área (OAC) + Área (OAB) ⇒
⇒ 16 = (4·r)/2 + (4·r)/2 +(4√2 ·r)/2 ⇒ 32 =(8 +4√2)r ⇒
⇒ 8 = (2 +√2)r ⇒ r = 8/(2 +√2) ⇒
⇒ r = 4 (2 -√2) ⇒ Área = 16π (2 -√2)2 cm2.
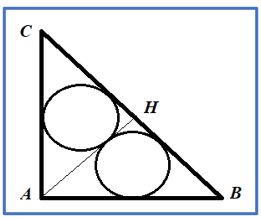
PROBLEMA 2.- Calcula el área de los círculos inscritos en un triángulo rectángulo isósceles, tangentes a dos lados del triángulo y tangentes entre sí en el que sus catetos miden 4 cm
Respuesta: El triángulo ABC queda dividido por la altura relativa a la hipotenusa AH en dos triángulos iguales, AHB y AHC cuyos catetos miden 2Ö2 cm, Por lo tanto, por semejanza, que es 1/√2, podemos decir que el área de cada uno de los círculos inscritos es la mitad del área del área del círculo del problema anterior, esto es: Área = 4π (2 -√2)2.
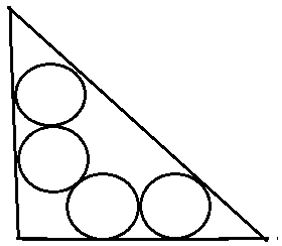
Problema 3 (propuesto): Calcula la suma de las áreas de los cuatro círculos inscritos en un triángulo rectángulo isósceles como indica la figura siguienteen el que sus catetos miden 4 cm
PROBLEMA 4.- El triángulo ABC es equilátero. Los círculos interiores son iguales y tangentes ente si el radio mide 2cm ¿Cuál es el área del triángulo?
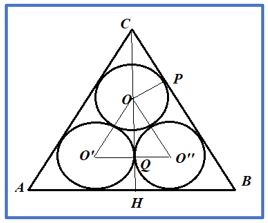
Respuesta: OP/OC = HP /CB= 1/2, ⇒ OC= 2OP = 2·r = 4 cm
El triángulo OO’O’’ es equilátero, Lado = OO’ = 2r = 4 y QO’’= r =2
OQ =√(42 -22) = 2√3 cm
La altura del triángulo equilátero ABC = CO + OQ + QH =
= 4 + 2√3 +2 = 6 + 2√3
Lado = (2/√3)(6 + 2√3) = (4√3 + 12)/√3 = (12 +12√3)3 = 4 + 4√3
Área = (4 + 4√3)( 6 + 2√3)/2 = (2 + 2√3)( 6 + 2√3) = 24 +16√3 cm2