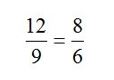El Álgebra supuso un avance importante en la historia de las matemáticas; los problemas de la geometría se podían abordar por procedimientos algebraicos y se podían resolver problemas que implicaban ecuaciones algebraicas de grado superior a dos. Algunos matemáticos, entre los que se encontraban J.Wallis (1616 – 1703) e I. Newton (1642-1727), llamaron al Álgebra Aritmética Universal, porque el Álgebra extendía la leyes de la Aritmética, permitía plantear y resolver problemas con más facilidad que con los métodos geométricos, se adaptaba mejor al estudio de la naturaleza y, además, permitía descubrir complejas relaciones matemáticas en el estudio de las Ciencias Físicas con más facilidad que con el uso de la Geometría Euclidiana.
Pocos dudaban que el Álgebra fuera una rama de las matemáticas, pero algunos matemáticos, como el maestro de Newton, I. Barrow (1558-1679), consideraban que el Álgebra era una rama de la Lógica, y era, simplemente ayuda del pensamiento. En el mismo sentido se manifestaba el filósofo Th. Hobbes (1588-1679) en una obra de 1660 en la que analizaba la Aritmética Universal de Wallis y concluía que el Álgebra no era ciencia sino un razonamiento simbólico. Podría ser que estas consideraciones fueran las que llevaron a Newton a redactar los Principia (1687) en el lenguaje geométrico, el cual era un método aceptado por todos y evitaba discusiones sobre problemas de forma, considerando que ya tendría bastante con defender la existencia de fuerzas de acción a distancia, como las gravitatorias.
Esta reacción se veía apoyada por algunas inconsistencias y paradojas que aparecían al resolver ecuaciones algebraicas, como, por ejemplo, cuando aparecían soluciones negativas; los números negativos presentaban paradojas como la siguiente:

En esta línea de paradojas lógicas y de reglas de cálculo no bien definidas hay que entender las críticas que realizó el obispo G. Berkeley (1685-1753) al Cálculo Infinitesimal y sus operaciones en su obra El Analista o un discurso dirigido a un Matemático Infiel (1734).

El Análisis Matemático se creó en el siglo XVII y sus fundamentos fueron publicados por primera vez por G. Leibniz (1646-1716) en la revista de Leipzig Acta Eruditorum en dos trabajos; Nova Methodus pro Maximis et Minimis (1984) y Geometría recóndita y análisis de los indivisibles e infinitos (1686).
Desde el primer momento se manifestaron críticas a la oscuridad de los fundamentos del Cálculo, en 1694, el Holandés B. Nieuventijt (1654-1718) lanzó una ataque en el que, aunque le reconocía a exactitud de los resultados obtenidos, decía que el método era oscuro y peligroso. La crítica de Nieuventijt tuvo una respuesta en defensa del método de los infinitesimales dada por el propio Leibniz en Acta Eruditorum.
Tras la publicación del primero libro de Cálculo Infinitesimal L’Analyse des Infiniments Petits (1696) de G. de L’Hôpital (1661-1704), se produjeron polémicas entre partidarios y detractores como la mantenida entre el crítico M. Rolle (1652-1719) y el defensor del cálculo P. Varignon (1654-1722).
Las críticas se sucedieron y ahora mostramos la crítica de Berkeley a la falta de rigor en los comienzos del Cálculo Infinitesimal. En su libro El Analista, Berkeley argumentaba de la siguiente manera: Supongamos que la cantidad x fluctúa uniformemente y nos proponemos calcular el diferencial de una potencia suya, xn. Al mismo tiempo que x se convierte en x + o, la potencia xn se convierte en (x+o)n. Desarrollando el binomio:
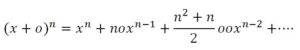
El incremento de xn es, por lo tanto:
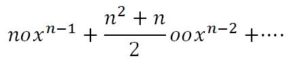
La relación entre los incrementos de x y de xn, que están en la relación de como 1 es a la siguiente cantidad

Y aquí viene el argumento que critica Berkeley: hagamos desaparecer los incrementos de su última proporción y quedará 1 es a nxn-1. Este razonamiento no es riguroso, pues al hacer que desaparezcan los incrementos, es decir, que no haya incrementos, se destruía la suposición primera de que los incrementos eran algo o de que hubiera incrementos y, pese a todo, se conservaba una consecuencia derivada de que los incrementos fueran algo, es decir, llegamos a una consecuencia derivada de una suposición o de algo que ya no existe.
Y alude a un lema de teoría de la demostración lógica que dice:
“Si en vistas a demostrar una proposición se supone cierto un punto, en virtud del cual pueden alcanzarse otros puntos y dicho punto de destruye o rechaza por un supuesto contrario, en este caso, todos los puntos, así alcanzados, y consecuentes, así como desde entonces en adelante, no pueden suponerse ni aplicarse más en la demostración”.
Pese a todas las deficiencias en sus fundamentos el Cálculo Infinitesimal en forma de algoritmo diseñado para el desarrollo de un razonamiento y sus aplicaciones al mundo de lo real alcanzó un desarrollo y una importancia enormes estableciendo relaciones entre diferentes medidas. Logro fundamental para el progreso y desarrollo de la Física que, gracias al Cálculo se convirtió en el nuevo modelo científico frente a las especulaciones de la filosofía tradicional.
El Cálculo desarrollado en el siglo XVIII cambió el sentido tradicional de la Física, que pasó, de ser filosofía de la naturaleza, a ser la ciencia que estudia los cuerpos materiales, en cuanto materiales. El Cálculo, pese a sus deficiencias lógicas, fue un soporte fundamental de la consolidación del método científico que en aquel momento tomaba cuerpo en la Teoría de la Gravitación Universal y las leyes de la Mecánica de Newton.

En 1784, la Academia de Berlín cuyo director era J.L. Lagrange , con el propósito de eliminar el uso de los infinitesimales, convocó un concurso para premiar la Memoria que proporcionara una teoría clara y precisa de lo que se llama infinito en Matemáticas. Porque según palabras de la convocatoria: es bien sabido que el la geometría superior se emplea habitualmente lo infinita grande y lo infinitamente pequeño… La Academia en consecuencia desea una explicación de cómo es posible que se hayan conseguido deducir tantos resultados correctos a partir de principios contradictorios, así de cómo… un concepto verdaderamente matemático puede sustituir al del infinito. El premio lo ganó, en 1786, S. L’Huilier (1750-1840) que desarrolló una teoría del Cálculo Infinitesimal basada en el concepto de límite.