El discípulo de Galileo B. Cavalieri (1598-1647) fue un matemático destacado entre los precursores del Cálculo Infinitesimal. Desde 1629, fue catedrático de Astronomía en Bolonia y en su obra Geometria continuorum indivisibilibus nova quadam ratione promota libri sex (1635) expuso método interesante para calcular áreas y volúmenes de figuras geométricas. Elaboró una teoría que se conoce como geometría de los continuos indivisibles.
Algunos matemáticos, como J. Kepler (1571-1630), calcularon el área del círculo, dividiéndolo en sectores de la misma amplitud y observando que, a medida que disminuía la amplitud de los sectores, si se disponían de forma conveniente, como se ve en la ilustración, se formaba una figura que se aproximaba, cada vez más, a un rectangulo cuya base era la longitud de la semicircunferencia y la altura el radio del círculo r. Con lo que concluyó que área del círculo era igual a la longitud de la semicircunferencia por el radio de la misma, esto es:
A = π·r·r = π·r2.
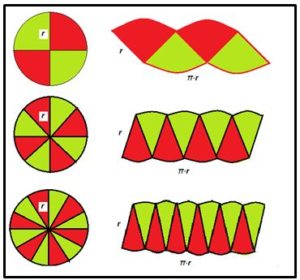
Puede observarse que si los sectores del círculo se disponen como se indica en la figura, a medida que la amplitud de los sectores tiende a cero, la figura que se forma se aproxima más y más a un rectángulo de largo π·r y de anchura r.
Kepler aplicó un método parecido al anterior para calcular el volumen de la esfera de radio R. Consideró una partición de la superficie esférica en partes infinitesimales y tomó cada una de ellas como base de una pirámide infinitesimal con la cúspide de cada una de ellas en el centro de la esfera. La altura de cada una de las pirámides infinitesimales es R. Como se sabía que el volumen de una pirámide era un tercio del producto de la superficie de la base por su altura.
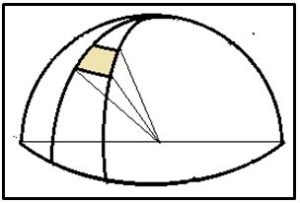
Al sumar todas las pirámides infinitesimales se obtenía que el volumen de la esfera era un tercio de la superficie A de la esfera por el radio R.
Volumen de la esfera = (1/3) A·R.
Cavalieri dio un paso en una dirección diferente ya que, Kepler y otros matemáticos, a la hora de medir superficies, las dividían en superficies más pequeñas y luego realizaban la suma de todas ellas. Y para medir volúmenes, los dividían en otros volúmenes más pequeños y luego calculaban la suma de todos ellos (es decir, dividían el volumen en otras figuras de la misma dimensión), Cavalieri supuso las que las figuras geométricas estaban formadas por elementos indivisibles de dimensión menor a la suya. Supuso que las líneas estaban formadas por puntos, que las superficies planas se podían dividir en infinitos segmentos rectilíneos paralelos a una recta fija y que los volúmenes se podían construir por unión de infinitos trozos de superficies planas equidistantes.
De este modo, Cavalieri aceptaba, de alguna forma, que la medida una superficie plana estaba relacionada con la suma de las longitudes de los infinitos segmentos rectilíneos que, para él, “formaban” la superficie, y que la medida de un volumen estaba relacionada con la suma de las áreas de los infinitos planos que formaban el volumen.
Esta idea no concordaba con las definiciones de línea y de superficie de la Geometría Clásica: La definición 2 de los Elementos de Euclides definía una línea como una longitud sin anchura y en la definición 4 de la misma obra se afirmaba que una superficie era lo que sólo tenía longitud y carecía anchura.
De estas definiciones se infería que, con adición de líneas sin anchura, no podía obtenerse ninguna superficie, ya que las líneas únicamente tenían longitud y las superficies tenían longitud y anchura y nadie aporta lo que no tiene. El mismo razonamiento podía aportarse a la imposibilidad de formar volúmenes por unión de superficies.
Cavalieri conocía perfectamente la Geometría de Euclides trató de salvar estas dificultades enunciando dos principios para calcular áreas y volúmenes.
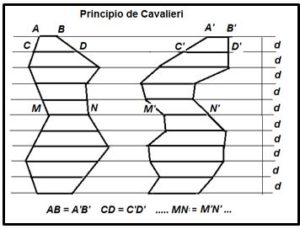
Primer Principio de Cavalieri: Si dos figuras planas están contenidas entre un par de rectas paralelas y si son iguales las longitudes de los dos segmentos determinados por la intersección de cualquier paralela con esas dos figuras, entonces las dos figuras tienen la misma área.
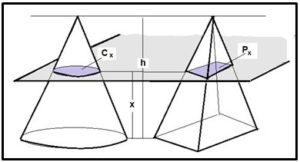
Segundo Principio de Cavalieri: Si dos sólidos están contenidos entre dos planos paralelos y si las áreas de dos secciones de estos sólidos cortadas por un plano paralelo a estos planos son iguales, entonces los dos sólidos tienen el mismo volumen.
La propuesta de Cavalieri no solamente chocaba con la Geometría de Euclides sino que también se le encontraron algunas paradojas como la siguiente:

Consideremos un triángulo ABC cuya altura BH lo divide en dos triángulos desiguales ABH y BHC, tal y como se observa en la figura. A cada indivisible NM del triángulo de ABH le corresponde un único indivisible de N’M’ del triángulo BHC de la misma longitud, y recíprocamente. y como los indivisibles correspondientes son iguales y están en el mismo número su suma también debería ser igual y, por tanto los triángulos ABH y BCH deben tener la misma área.
Los métodos de Cavalieri recibieron las críticas de muchos matemáicos. P. Guldin (1577– 1643) criticaba el método porque el uso del infinito era una metodología no constructiva que quedaba fuera de los métodos de la Geometría de Euclides. Sin embargo, el método de Cavalieri fue elogiado por otros matemáticos como E. Torricelli (1608-1747) que vio en el método, pese a los problemas lógicos, un procedimiento ágil para cálcular áreas y volúmenes.
Los métodos de Cavalieri tuvieron una popularidad notable porque permitían demostrar con facilidad resultados ya conocidos, a los que se había llegado mediante procedimientos más laboriosos. Como es el caso del cálculo del volumen de la esfera demostrado por Arquímedes. Para calcular el volumen de la esfera el sabio de Siracusa relacionó el volumen de una semiesfera con el de un cilindro circular recto y con el de un cono recto (ambos de base igual a un círculo máximo de la semiesfera). Cavalieri calculó el volumen de la esfera de la forma que se expone a continuación:
En un cilindro recto de radio R y de altura R, están inscritos un cono recto de radio R y altura R y una semiesfera de radio R tal y como se muestra en la figura:

Un plano paralelo a la base del cilindro trazado a una distancia h de la cúspide del cono determina tres círculos: un círculo radio R con el cilindro, otro círculo de radio r con la semiesfera y otro círculo de radio h con el cono (basta observar que DEF es un triángulo rectángulo isósceles).
En la figura se puede observar que el triángulo rectángulo EGH es rectángulo y se cumple que r2 + h2= R2. Por tanto multiplicando por π se obtiene que:
πr2 + πh2= πR2.
Área del círculo de la semiesfera + Área del Círculo del cono = Área del Círculo del cilindro
Aplicando el Segundo Principio de Cavalieri se deduce que :
Volumen de la semiesfera + Volumen del cono = Volumen del cilindro
Despejando:
Volumen de la semiesfera = volumen del cilindro – volumen del cono
Como lor volúmenes del cilindro y del cono eran conocidos, se tiene que:
Volumen de la semiesfera = πR3– πR3/3 = 2πR3/3
Luego
Volumen esfera = 4πR3/3.
Método más sencillo que el de Arquímedes aunque alejado del rigor geométrico.