El problema de la trisección de un ángulo cualquiera es, junto con la cuadratura del circulo y la duplicación del cubo, uno de los Tres Problemas Clásicos Griegos. Se trataba de encontrar un procedimiento para dividir en tres partes iguales un ángulo cualquiera, pero utilizando solamente la regla y el compás.
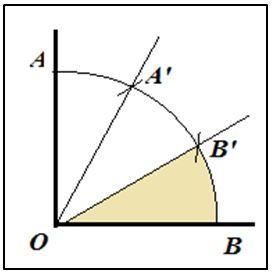
Trisecar un ángulo recto AOB era un problema elemental, como puede observarse en la figura y se procede así: Con centro en el vértice O y con un radio arbitrario OA se traza el arco AB. Luego, con centro en B y con el mismo radio se obtiene A’, finalmente, con centro en A y el mismo radio se obtiene B’. Las semirrectas OA’ y OB’ trisecan el ángulo recto AOB.
El método utilizado para trisecar el ángulo recto no servía para todos los ángulos y no se encontraba un método para hacerlo utilizando solamente la regla y el compás. Un método muy sencillo, que se le atribuye a Arquímedes, es el siguiente: Sea AOB el ángulo que deseamos trisecar.
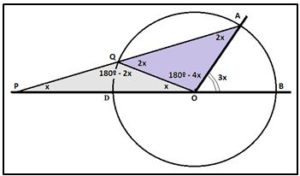
Construcción:
- Trazamos una semicircunferencia, con centro en O y radio arbitrario, r, que corta a los lados del ángulo AOB en A y en B. Por lo tanto: r = OA = OB.
- Prolongamos el lado OB del ángulo AOB en un recta, que llamaremos s, que corta a la semicircunferencia en los puntos B y D.
- En una regla, señalamos una distancia igual al radio de la semicircunferencia. Sean P y Q estas marcas sobre la regla. Por lo tanto: r = PQ.
- Colocamos la regla de tal modo que Q coincida con algún punto de la semicircunferencia y P con algún punto de la recta s y que, al mismo tiempo, la regla pase por A. Entonces el ángulo APB es la tercera parte de AOB.
Para demostrar que es verdadera la afirmación que acabamos de hacer, hagamos las sigu ientes consideraciones: El triángulo OQP es isósceles porque QP = QO = r, y, por tanto: ángulo QPO = ángulo QOP = x. Lo cual implica que: ángulo AQO = ángulo QAO = 2x.
Finalmente AOC = 3x. Por lo que el ángulo APB es la tercera parte del ángulo AOB.
Esta forma de resolver el problema no era válida porque, según las exigencias de la resolución de problemas con el uso exclusivo de la regla y el compás, la regla sólo se debía utilizar para trazar rectas y no para realizar o transportar medidas y, por lo tanto, la regla no debe ser graduada ni tener marcas.
El problema quedó abierto sin que nadie obtuviera una solución correcta durante siglos. Se plantearon muchas dudas sobre si la resistencia del problema se debía a la impericia de los matemáticos o era un problema que no podía resolverse bajo las premisas de la construcción con regla y compás. Hasta que en el siglo XIX, utilizando el lenguaje algebraico, se logró demostrar que el problema de la trisección del ángulo no tenía solución porque en los términos planteados con el uso de la regla y el compás.
Se demostró que no se podía trisecar el ángulo de 60º, porque equivalía a la resolución de una ecuación cúbica sin ninguna raíz racional, como se muestra a continuación:
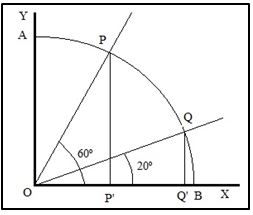
Sea el ángulo de 60º POB, donde OB está en el eje OX y APQB el cuadrante de a circunferencia unidad. Trisecar ese ángulo supondría poder determinar un punto Q tal que la recta que OQ forme con el eje OX un ángulo de 20º.
Ese punto P tendría de coordenadas (cos 60º, sen 60º) y Q (cos 20º, sen 20º). Podríamos relacionar algebraicamente los ángulos mediante su coseno un ángulo α con su tercera parte mediante la fórmula trigonométrica:
Cos α = 4 cos3 (α/3)- 3 cos (α/3)
Haciendo z = 3 cos (α/3) y α = 60º, la ecuación trigonométrica se transforma en:
4z3 – 3z = 1/2 o, equivalentemente, en la ecuación 8z3 – 6z = 1
Esta es una ecuación cúbica con coeficientes racionales que no tiene raíces racionales y se puede demostrar que si una ecuación cúbica con coeficientes racionales no tiene una raíz racional, entonces ninguna de sus raíces es construible partiendo de Q, Es decir, como la ecuación cúbica 8z3 – 6z = 1 tiene coeficientes racionales y no tiene ninguna raíz racional, entonces ninguna de sus raíces se puede construir con regla y compás a partir de elementos de Q.
El problema de la trisección del ángulo siguió fascinando a los matemáticos mucho tiempo en 1899 el matemático anglo americano F. Morley (1860-1937) demostró un hermoso teorema sobre las propiedades de las trisectrices de los ángulos de un triángulo que lo podemos formular así: Los tres puntos intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero.
Acabaremos mostrando una manera muy curiosa de trisecar un ángulo trasladando el problema en el plano a tres dimensiones, y trisecar un ángulo cualquiera en el plano con ayuda de una superficie cónica de la siguiente forma (según se señala en la figura):
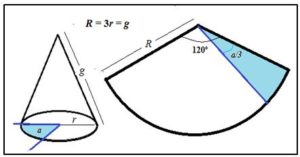
1.- Consideremos un círculo de radio r y un sector circular de 120º de amplitud y un radio R = 3r .
2.- Es evidente que la longitud de la circunferencia del circulo de radio r es 2𝜋r y la longitud del arco del sector será la misma (6𝜋r/3).
3.- Con el sector de radio R podemos hacer un cono, cuyo radio de la base es r y su generatriz R =3r
Si deseamos trisecar un ángulo a lo dibujamos sobre el círculo de radio r colocando el vértice del ángulo en el centro del círculo. A continuación colocamos el cilindro sobre el círculo haciendo coincidir la circunferencia del mismo con la base del cono. Luego marcamos sobre la superficie cónica la abertura del ángulo a. Al desarrollar la superficie cónica los puntos marcados darán sobre el sector un ángulo de a/3.




