EL PEQUEÑO TEOREMA DE FERMAT

Pierre  Fermat (1601- 1665) fue, sin duda, uno de los matemáticos franceses más grandes del siglo XVII. Fue, junto con R. Descartes (1596-1650), uno de los creadores de la Geometría Analítica; también mantuvo una activa correspondencia con B. Pascal (1623-1662) sobre la resolución de los problemas relacionados con el reparto de apuestas planteados por el caballero de Meré y que dieron lugar al nacimiento de la teoría matemática del Cálculo de Probabilidades.  Además, Fermat fue uno los precursores del Cálculo Infinitesimal, estudiando el trazado de tangentes a curvas expresadas en forma analítica y las condiciones de máximo y mínimo con el método que hoy llamamos derivadas. Con este método, descubrió en la Óptica Geométrica (con la hipótesis de que cuando la luz viaja por un medio más denso su velocidad disminuye) el conocido como Principio de Fermat que afirma que la trayectoria entre dos puntos de un rayo luminoso es aquella que tarda menos tiempo en recorrerla; de este Principio se deducen las leyes de la reflexión y la refracción de la luz.

Pero el tema que había de dar a Fermat renombre universal fue la conocida como Conjetura de Fermat, que acabaría siendo conocida como último Teorema de Fermat y que tardaría más de tres siglos en demostrarse. Su interés por la Teoría de Números empezó hacia 1630 mientras estudiaba la traducción de la Aritmética de Diofanto (siglo III) realizada por C. Bachet de Méziriac (1581-1638). Realmente Fermat realizó profundas investigaciones y desarrolló diferentes métodos (como el del descenso infinito), pero, sin duda, su resultado más popular fue el que escribió en el margen de la Aritmética de Diofanto, al lado del problema 8 del libro II que dice: Dado un número cuadrado, descomponerlo en suma de otros dos números cuadrados. Ahí escribió su famosa conjetura: Es imposible que un cubo se pueda expresar como una suma de dos cubos o que una cuarta potencia se exprese como una suma de dos cuartas potencias y, en general, es imposible que una potencia de grado n mayor que dos se pueda descomponer como suma de dos potencias de grado n. Y concluye que con algo que se ha considerado como un desafío matemático durante tres siglos y medio: He encontrado una demostración verdaderamente maravillosa de este resultado, pero este margen es demasiado estrecho para contenerla. En suma, Fermat conjeturó que la ecuación xⁿ + yⁿ = zⁿ no tiene soluciones enteras positivas para n > 2.

Entre la formulación de la Conjetura en la década de los treinta del siglo XVIII y mayo de 1995, fecha en la que Andrew Wiles (1953-) publicaba en la revista Annals of Mathematics su demostración definitiva hay siglo y medio. Puede decirse que el estudio metódico de las propiedades de los números enteros comenzó realmente con Fermat, razón por la que ha sido considerado el verdadero creador de la teoría de los números

Hoy vamos a exponer la demostración y algunas aplicaciones del conocido como Pequeño teorema de Fermat, para la demostración realizaremos una aproximación elemental siguiendo el texto de Hall, H.S. y S.R.  Knight Algebra superior. Empezaremos con dos lemas introductorios:

LEMA 1.- Si p  es un número primo, los coeficientes de cada término del desarrollo del binomio (a + b)^p, excepto el primero y el último, son múltiplos de p [M(p)].

Demostración: El desarrollo de (a + b)^p es:

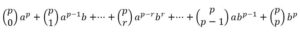
Ese es el coeficiente del término (r+1)-ésimo es un número entero, por lo tanto, el denominador divide al numerador.

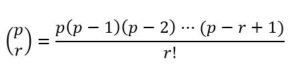
Hagamos las siguientes consideraciones: r puede tomar valores de 1 a p-1.

Como p es primo ningún factor de r! divide a p, pero como p > r, p tampoco divide a r, no puede ser factor suyo. Por lo tanto el denominador, r!, no divide a p y como el   coeficiente del término r+1-ésimo y es un número entero quiete decir que r!,  divide a (p-1)(p-2)···(p-r+1) es decir :

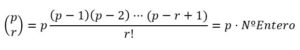
Luego son múltiplos de p 

LEMA 2.- Si p es un número primo, y a, b, c,… n sumandos, entonces:

(a + b + c + ···)^p = a^p + b^p + c^p + ··· + M(p)

Demostración: Llamando β = b + c + ···, se tiene por el lema 1:

(a + b + c + ···)^p = (a + β )^p = a^p + β ^p + M(p)

Llamando γ =  c + d + ···,

β ^p=(b + c + ···)^p= (b + γ)^p = b^p + γ ^p + M(p),  ⇒

(a + b + c + ···)^p = a^p + b^p + γ ^p + M(p), repitiendo el proceso se obtiene la tesis.

Pequeño Teorema de Fermat.  Si p es un número primo y no divide a N, entonces N^p-1 – 1 es múltiplo de p.

Demostración: Si en (a + b + c + ···)^p = a^p + b^p + c ^p ··· + M(p),  hacemosd:

a = b = c = ··· = 1

N^p = N + M(p)  o   N^p – N =  M(p)

N(N^p-1 – 1) = M(p)

Si N y p son primos entre si, entonces, p no divide a N, y por tanto,  N^p-1 – 1 = M(p)

OBSERVACIÓN: En la demostración del pequeño teorema de Fermat hemos visto que para cualquier N se cumple que: N^p – N =  M(p)

PROBLEMA 1 .- Demostrar que n⁷ – n es divisible por 42.

Solución: Por la observación sabemos que si p es primo N^p – N =  M(p), luego n⁷ – n es múltiplo de 7.

Por otra parte, descomponiendo n⁷ – n

n⁷ – n = n (n⁶ – 1) = n (n² – 1) (n⁴ + n²+1) = n (n – 1)(n+1) (n⁴ + n²+1)

Como n es un entero cualquiera en el producto n (n – 1)(n+1) (de tres enteros consecutivos) hay, al menos un par, por lo tanto es divisible por 2 e, igualmente, n (n – 1)(n+1) hay un múltiplo de 3, por lo tanto  n⁷ – n es divisible por 7·2·3 =42

PROBLEMA 2 .- Demostrar que para todo número primo n mayor que 5  n⁴ – 1 es divisible por 240

Solución: n⁴ – 1 = (n+1) (n-1) (n²+1).

Por una parte:

Como n es primo y mayor que 5, entonces n es impar (2 es el único número primo par). Por lo tanto, (n+1) y (n-1) son dos números pares consecutivos, por lo tanto,  el producto de ambos será múltiplo de 8, además, el otro factor, (n²+1) es  también par, por consiguiente, n⁴ – 1 es múltiplo de 16.

Como n es primo (mayor que 5), entonces n y 5 son primos entre si y, aplicando el pequeño Teorema de Fermat, se sigue que n⁴ – 1 es múltiplo de 5.

Finalmente, n⁴ – 1 = (n² – 1) (n² +1), entonces, observando el factor (n² – 1), como n y 3 son primos entre si y, aplicando el pequeño Teorema de Fermat, se sigue que n⁴ – 1 es múltiplo de 3.  Por consiguiente, n⁴ – 1 es múltiplo de 16·5·3 = 240

PROBLEMA 3.-.- Demostrar que para todo número primo n mayor que 3, excepto 7,  se cumple que n⁶ – 1 es divisible por 168

Solución: Por el pequeño Teorema de Fermat  n⁶ – 1, es divisible por 7 salvo si n =7, ya que, en ese caso, el número primo 7 divide a la base.

Por otra parte n⁶ – 1 = (n² – 1) (n⁴ + n²+1),  luego n⁶ – 1 es divisible por (n² – 1), por lo tanto, si n  es primo mayor que 3 será impar y  (n² – 1) = (n+1)(n-1) producto de dos pares consecutivos y, por tanto,  divisible por 8. Luego n⁶ – 1, es divisible por 8.

También por el pequeño Teorema de Fermat (n² – 1) es divisible por 3.

Luego  n⁶ – 1,  es divisible por  7·8·3=  168