PROBLEMA 1.- Dos jugadores A y B extraen bolas alternativamente con reemplazamiento de una urna que contiene 5 bolas blancas y 10 bolas negras. Ganará el jugador consiga extraer una bola blanca. Calcular las respectivas probabilidades de que gane cada uno de los jugadores.
Solución : Supongamos que empieza a extraer bolas el jugador A. Por el enunciado, podría ganar en su primera extracción con una probabilidad 5 /15 y acabar la partida, pero si obtuviera negra, aun puede ganar en una segunda oportunidad si B saca negra y A saca blanca lo que tiene una probabilidad de (10 /15)· (10 /15)· (5 /15) y aún puede ganar en una tercera posibilidad, cuarta o quinta.
Si llamamos Ak al suceso Ak= {la primera bola blanca aparece en la extracción k}.
La extracción k del jugador A supone que antes ha habido k-1 extracciones fallidas en las que ha obtenido bola negra.
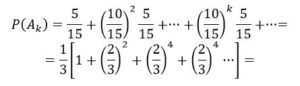
Por lo tanto, la probabilidad que gane A será:
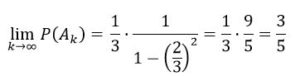
La probabilidad de que gane B será 2/3
PROBLEMA 2.- Dos jugadores A y B extraen bolas alternativamente con reemplazamiento de una urna que contiene a bolas blancas y b bolas negras. Ganará el jugador consiga extraer una bola blanca. Calcular las respectivas probabilidades de que gane cada uno de los jugadores.
Solución: Sea Ak el suceso {la primera bola blanca aparece en la extracción k}.
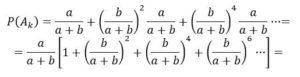
Por lo tanto, la probabilidad que gane A será:
Probabilidad de que gane el contrincante P (gane B) = 1- P (gane A) = b/(a+2b)
PROBLEMA 3. Se colocan al azar n bolas en n urnas. Calcular las probabilidades siguientes situaciones:
a) De que las n urnas queden ocupadas b) De que quede una sola urna determinada vacía
Solución:
a) Para que estén todas las urnas ocupadas tiene que haber una bola en cada urna. El número de casos favorables será el número de modos diferentes de colocar una bola en cada urna (permutaciones sin repetición de n elementos), CF = Vn, n = n! y el número de casos posibles será el número de modos diferentes de acomodar las n bolas en las urnas (una urna con todas las bolas, tres urnas vacías, etc), es decir, variaciones con repetición de n elementos tomados de n en n.
CP = VRn, n = nn.
Por lo tanto, la probabilidad será:
b) El número de casos posibles es nn , que es el número de variaciones con repetición de n elementos tomados de n en n.
Para contar los casos favorables procederemos así:
- Tenemos n formas de elegir la urna que queda vacía (por ejemplo, la primera)
- Como las demás urnas han de contener alguna bola, una de las n-1 ocupadas debe contener dos bolas.
- Como las bolas son diferentes seleccionaremos entre las n bolas dos de ellas (para introducir en esa urna) lo que nos dará C n,2 parejas
- Por último, podemos colocar las n-2 bolas restantes en las n -2 (urnas de (n-2)! formas
CF = n(n-1) C n,2· (n-2)!
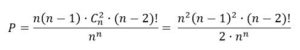
PROBLEMA 4. Distribuimos al azar n bolas blancas y n bolas negras en n urnas.
a) Hallar la probabilidad de que una urna determinada contenga i bolas blancas y j bolas negras.
b) Calcular la probabilidad de que en cada urna haya una bola de cada color.
Solución
Solución a) Consideremos que a cada bola de damos un vale con un número de 1 a n que le indica la urna en la que tiene que introducirse. Entonces:
Casos posibles son: CP = VRn, 2n = n2n
Casos favorables: Supongamos que la urna elegida es la primera, meteremos en ellas i bolas blancas, que podemos elegir de Cn,i, formas diferentes y j bolas negras que que podremos elegir de Cn, j formas distintas. Finalmente, repartimos el resto de bolas, que serán n-i-j, en el resto de las urnas, n-1 urnas, que lo podremos hacer de RVn -1, n-i-j formas diferentes, por tanto:CP = C n,i·C n,j· RV n-1, n-i-j = C n,i·C n,j·(n-1) n-i-j
b) Tanto las bolas blancas, como las negras se pueden distribuir en las n urnas de n! maneras posibles. Por lo tanto:
