LA INFINITUD DE LOS NÚMEROS PRIMOS Y EL MÉTODO DE REDUCCIÓN AL ABSURDO

La primera demostración de que el conjunto de los números primos era infinito apareció por primera vez en los Elementos de Euclides. La matemática griega no aceptaba como la existencia real de conjuntos infinitos y a los números naturales, a los pares, o a los números racionales los consideraba simplemente conjuntos indefinidos o, en terminología aristotélica, que eran infinitos solamente en sentido potencial, sin que tuvieran existencia completa en el ámbito real, ni en el mundo del pensamiento.

Zenón de Elea es considerado el inventor de la Dialética con un método de demostración conocido como   Método de Reducción al Absurdo, mediante el que prueba la verdad de una proposición por la imposibilidad de aceptar las consecuencias que se derivan de su negación tomada como hipótesis. Para demostrar que p → q    se debía probar que la hipótesis: “p y (no-q)”  implicaba una contradicción y que, por lo tanto, se debía verificar la implicación directa p → q. El método apareció de la Escuela Pitagórica y se apoyaba en la idea de que una contradicción era inadmisible en un sistema lógico. Fue utilizado para demostrar la inconmensurabilidad de la diagonal de un cuadrado con su lado, es decir, que el número o que √2 no era un número racional. Sin embargo, pese a su origen pitagórico, la Escuela de Elea lo usó y con gran maestría contra las concepciones físicas de la Escuela Pitagórica.

Este método aparece en Los Elementos de Euclides en la prueba de la demostración de que los números primos son infinitos. En la Proposición 20 del Libro IX, formulada de la siguiente forma: Hay más números primos que cualquier cantidad propuesta de números primos.

Se han hecho muchas demostraciones, a continuación mostramos dos:

Demostración 1:

Supongamos que p es el mayor primo de todos los existentes; entonces el producto: 2·3·5·7 ··· p, es divisible por cada uno de los primos, por lo tanto: 2·3·5·7 ··· p + 1, no es divisible por ninguno de los primos existentes. Por consiguiente, o es un número primo o es un número compuesto o es divisible por un primo mayor que p. En cualquier caso, p no es el mayor de los números primos y, por lo tanto, el conjunto de los números primeros es ilimitado

Demostración 2: de Euclides

Sean a, b, c la lista de números primos propuestos.  Sea AE el número menor medido por a, b, c (en realidad, a·b·c) y le añadimos una unidad EZ, entonces AZ o es primo o no. Si es primo hay más que los que hemos supuesto, Supongamos que no es primo, evidentemente, si no es primo tendrá que ser divisible por un número primo que no sea a, b, c. Suena raro, pero en notación moderna escribiríamos:

Si el conjunto de números primos tiene n elementos P = {p₁, p₂, p₂, … p_n}es un conjunto finito de números primos, entonces P no contiene a todos los números primos.

El menor número que se puede dividir por todos ellos será el producto: n = p₁· p₂· p₂, ··· p_n. Consideremos el número n +1. Este número o es primo o es divisible entre un primo. Si n+1 es primo, evidentemente, no está en P y como P es un conjunto cualquiera de primos, el resultado está probado.

Supongamos n+1 no fuera primo; quiere decir que existirá un primo, p.  que divide a n+1, pero, entonces, p no puede pertenecer  a  P, ya que,  si perteneciera, dividiría a n  (ya que n = p₁· p₂· p₂, ··· p_n ) y,  como suponemos que divide a n+1, también dividiría a su diferencia (n+1) – n =1, lo cual es imposible y, por tanto, hemos encontrado un primo (n +1) que no pertenece  P.

Problema: Sea  π(n) el número de factores primos distintos en la descomposición del número natural n. Por ejemplo  π(2) = 1,  π (6) =p (2×3) = 2,  π (8) = π (2³) = 1, demostrar que

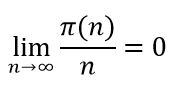
Demostración: Sea n un número natural y (con un abuso de notación) escribiremos

n = (a₁)^a·(a₂)^b ·(a₃)^c ···(a_r)^r,  donde a₁, a₂, a₃, ···, a_r son números primos. Tomando logaritmos:

Ln n = Ln (a₁)^a + Ln (a₂)^b + Ln (a₃)^c + ··. + Ln (a_r)^r  = a Ln (a₁) + b Ln (a₂) + c Ln (a₃) + ··. + r Ln (a_r)

Como los exponentes son mayores que 1:

Ln n ≥ Ln (a₁) +  Ln (a₂) +  Ln (a₃) + ··. +  Ln (a_r)

Como a₁, a₂, a₃, ···, a_r son mayores o iguales que 2

Ln n  ≥ p (n)·Ln2  ⇒ (dividendo entre n)

Pero como π(n)/ n es positivo, el límite es cero lo que significa que, aunque  π(n), tiende a infinito crece mucho más lentamente que n.