Si un número termina en ceros quiere decir que en su descomposición en factores primos están los factores dos y cinco. Es evidente que si N = 2ª·5b·xc·yd… el número de ceros en que termina N será igual al menor de los exponentes a y b de los números primos 2 y 5. Así el número N = 23·3·52·112·17 acaba en dos ceros porque 2 = min {3, 2}Si se calcula resulta que N = 1.234.200.
Para de calcular el número de ceros en que termina n! = n·(n-1)·(n-2)···3·2·1. Pensemos que este número es producto de factores, pero no son todos primos. En n! los factores 2 y 5 aparecerá una vez, pero otros factores también los contienen, por ejemplo 4 y 6 contienen al dos; 15 y 25 contienen al cinco, 10 y 50 contienen al dos y al cinco, etc…)
Debemos observar que, dado que en n! = n·(n-1)·(n-2)···3·2·1, hay más factores pares que múltiplos de cinco, luego para conocer el número de ceros en que termina n!, bastará con calcular los múltiplos de cinco y su comportamiento. Los múltiplos de cinco son: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 100,…,115, 120, 125, …, 625,…
El número factores múltiplos de 5 que tiene n! será la división entera de n/5, es decir, en la que tomamos el cociente sin decimales. Que en notación Excel será: =COCIENTE (n;5)
Así, 853! tiene: = COCIENTE (853;5) = 170 múltiplos de cinco, pero, entre esos múltiplos de cinco, hay factores que son múltiplos de 25 (25, 50, 75..) y tienen dos factores cinco y otros factores que son múltiplos de 125 (125, 250, 375, ..) que tienen tres factores cinco… Para contar los factores cinco que tiene n! se deben determinar los múltiplos de las potencias de 5 desde 1 hasta n y sumarlos.
Ejemplo1: ¿En cuántos ceros acaba 853! = 853·852 ···· 3·2·1?
Entre sus factores hay:
- =COCIENTE (853:5) = 170, múltiplos de cinco que, por lo menos, aportan un cinco cada uno.
- =COCIENTE (853:25) = 34, múltiplos de veinticinco que, por lo menos, aportan dos cincos cada uno (aunque uno está contado en los múltiplos de cinco)
- =COCIENTE (853:125) = 6, múltiplos de ciento veinticinco que, por lo menos, aportan tres cincos cada uno (aunque dos están contados en los múltiplos de veinticinco)
- =COCIENTE (853:625) = 1, múltiplos de seiscientos veinticinco que por lo menos aportan cuatro cincos cada uno (aunque tres están contados en los múltiplos de ciento veinticinco)
Luego el número de factores cinco de 853! será la suma de los cocientes obtenidos:
170 + 34 + 6 + 1 = 211, por lo tanto, 853! acabará en 211 ceros.
Se puede agilizar el procedimiento realizando divisiones enteras sucesivas como se ve a continuación
Ejemplo 2: Determina en cuántos ceros termina 2999!
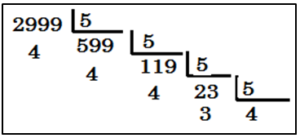
Si hacemos la división entera de 2999 entre 5, obtenemos un cociente 599; si a continuación hacemos la división entera de 599 entre 5 (que es como si la hacemos la división entera de 2999 entre 25) obtenemos un cociente 119 y así sucesivamente hasta que el cociente obtenido sea menor que 5. La suma de los cocientes de las divisiones enteras sucesivas: 599 + 199 + 23 + 4 = 825 nos dará el número de ceros en que termina 2999!