Los números de nuestro sistema de numeración formados íntegramente por la misma cifra repetida tienen muchas propiedades curiosas que pueden ser utilizadas en la enseñanza para despertar la curiosidad y el interés de los estudiantes por la Aritmética. Basta saber que un número es divisible por tres (o que es múltiplo de tres) cuando la suma de sus cifras es tres o múltiplo de tres) para responder a sencillas cuestiones:
Cuestión 1.- ¿Cuál es el menor número menor que mil con tres cifras iguales que sea múltiplo de tres? [Evidentemente, 111] que da pie a plantear otras cuestiones como:
Cuestión 2.- ¿Cuántos números de tres cifras menores que 111 son múltiplos de tres? Evidentemente, por ser los números buscados de tres cifras, tienen que ser mayores que 100 y menores que 111, como 102 es el primer múltiplo de tres de tres cifras, buscamos los múltiplos de tres comprendidos entre 102 y 111, El este caso como no entra el 111, serán (111-102)/3 = 1+ 3 = 4. (102, 105, 108)
Cuestión 3.-¿Cuál es el menor número menor que un millón con seis cifras iguales que sea múltiplo de tres? [Evidentemente, 111111],
Cuestión 4.- ¿Cuántos números de tres cifras menores que 111111 son múltiplos de tres? [(111111-100008)/3 = 11103/3 = 3701]
Cuestión 5.- ¿Cuál es el menor número menor que un millón con seis cifras iguales que sea múltiplo de nueve? [Evidentemente, 333333]
Cuestión 6.-¿Cuántos número de seis cifras menores que 333333 son múltiplos de tres? [(333333 – 100008)/3 = 233325/3 = 77775]
Paso a describir algunas propiedades:
Propiedad primera: Los cuadrados de los números cuyas cifras son la unidad, son números capicúas, de la forma siguiente:
12 = 1
112 = 121
1112 = 12321
11112 = 1234321
111112 = 123454321
1111112 = 12345654321
11111112 = 1234567654321
111111112 = 123456787654321
1111111112 = 12345678987654321
¿Es capicúa 111111111112 ?
Propiedad segunda: El primer número con nueve cifras iguales que es múltiplo de nueve es 111.111.111 (la suma de sus cifras es nueve). Este número tiene una propiedad importante y es que dividido entre 9 resulta este curioso número: 12.345.679, es decir, está formado por las cifras escritas en orden creciente sin el cero y sin el ocho. Esto es, cumple que: 111.111.111 = 9 x 12.345.679.
Esto da una propiedad curiosa que se ha empleado en juegos de Salón para realizar una operación que suele sorprender, haciendo lo siguiente:
Tomemos el número 12345679 y se le dice a una persona cualquiera de la reunión que elija una cifra del 1 al 9. A continuación se le dice que vamos a hacer un truco de magia, que consiste en que va a multiplicar con la calculadora el número 12345679 por otro número que se le dirá y que obtendrá un número que sólo contendrá la cifra que tú has elegido.
Si ha elegido la cifra 5 le diremos que multiplique 12.345.679 por 45 de ese modo:
12.345.679 x 45 = 12.345.679 x 9 x 5 = 111,111.111 x 5 = 555.555.555
En general, si ha elegidla cifra a le diremos que multiplique 12.345.679 por (9xa) y tendremos:
12.345.679 x (9xa) = (12.345.679 x 9) x a = 111,111.111 x a = aaa.aaa.aaa
12345679 x 9 = 111111111
12345679 x 18 = 222222222
12345679 x 27 = 333333333
12345679 x 36 = 444444444
12345679 x 45 = 555555555
12345679 x 54 = 666666666
12345679 x 63 = 777777777
12345679 x 72 = 888888888
12345679 x 81 = 999999999
Problema análogo al anterior: Dado que 111111111111111/3 =37037037037037 o, lo que es equivalente: 37.037.037.037.037×3 = 111.111.111.111.111 ¿Por que número hay que multiplicar 37.037.037.037.037 para obtener un número con todas las cifras iguales.
Propiedad tercera: Es fácil comprobar:
98 x 9 = 987 x (10-1) = 980- 98 = 882
987 x 9 = 987 x (10-1) = 9870- 987 = 8883
9876 x 9 = 9876 x (10-1) = 98760- 9876 = 88884
98765 x 9 = 98765 x (10-1) = 987650- 98765 = 888885
987654 x 9 = 987654 x (10-1) = 9876540- 987654 = 8888886
9876543 x 9 = 987654 x (10-1) = 98765430- 9876543 = 8888887
98765432 x 9 = 98765432 x (10-1) = 987654320- 98765432 = 8888888
Y por tanto:
98 x 9 + 6= 987 x (10-1) +6 = 980- 98 + 6 = 888
987 x 9 + 5= 987 x (10-1) + 5= 9870- 987 + 5 = 8888
9876 x 9 +4= 9876 x (10-1) +4= 98760- 9876 + 4= 88888
98765 x 9 + 3= 98765 x (10-1) + 3 = 987650- 98765 + 3= 888888
987654 x 9 + 2 = 987654 x (10-1) + 2 = 9876540- 987654 + 2 = 8888888
9876543 x 9 + 1 = 987654 x (10-1) + 1 = 98765430- 9876543 + 1 = 8888888
98765432 x 9 + 0 = 98765432 x (10-1) + 0 = 987654320- 98765432 + 0 = 8888888
Popiedad cuarta : A partir de la tabla en la que se indican los restos de las divisiones demostrar
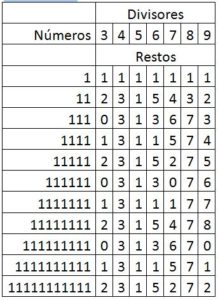
a) Si a un número con todas las cifras iguales le restamos una unidad resulta múltiplo de dos y de cinco
b) Si a 1111…11 le restamos 3 unidades resulta múltiplo de 4
c) Si a un número formado por todo unos mayor que 11 le restamos siete es divisible por cuatro y por ocho.
Problema.- Demuestra que existen números con todas las cifras iguales que son múltiplos de 13. Además esta cifra puede ser cualquiera.
Respuesta: Consideremos los números, formados por unos:
1, 11, 111,…, 11..14 cifras..1 [1]
Llamemos a los números a1, a2, a3,….., a14 respectivamente
Si alguno de esos catorce números fuera múltiplo de 13, el problema ya estaría resuelto, ya que ese sería el número que buscamos. Veremos que uno de ellos será divisible por 13:
Sabemos que cuando se divide cualquier número entre 13 sólo puede dar uno de los siguientes veintinueve restos diferentes: 0, 1, 2,…., 12
Por lo tanto, entre los restos obtenidos en las divisiones de los treinta números de [1] entre 13 debe haber al menos dos restos iguales. Sean éstos los números
aj = 11.. j cifras ..1 y ak = 11.. k cifras ..1 y j > k
La diferencia de ambos será un número formado por j-k unos y k ceros que será divisible por 13:
x = 11 … j –k … 1 00… k cifras … 0
El número x es múltiplo de 13 , pero no tiene las cifras iguales como nos exige el enunciado. No obstante, admite la descomposición en el producto de los dos factores
x = 11 … j –k ... 1 X 100 k cifras 0
Como 13 divide a x y no divide al factor 100 k cifras 0 (ya que sólo tiene como factores primos el 2 y 5), necesariamente dividirá al otro factor, es decir a:
11 … j –k cifras … 1
Que es un número de la lista formado por cifras j-k iguales, es decir, el número aj-k, que tiene j-k unos el que es divisible por 13,. Si ese número es divisible por 13, también lo sera el que tiene j-k cifras repetidas.