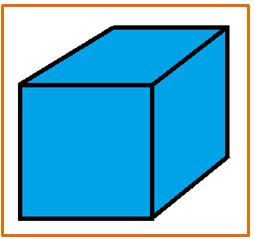
Plantearemos un problema sencillo, el de contar los elementos de una colectividad ordenada en la que hay diferentes elementos con diferentes características.
Imaginemos un cubo de madera de lado L, lo pintamos de azul y luego lo dividimos en cubos iguales de lado L/n
¿En cuántos cubitos habremos dividido el cubo original?
¿Cuántos cubitos habrá con una cara azul?
¿Cuántos tendrán dos caras azules?
¿Cuántos tendrán tres caras azules?
¿Cuántos habrá sin ninguna cara pintada?
Observaremos que el cubo original (como todos los cubos) tiene seis caras, ocho vértices y doce aristas y recordemos que los poliedros convexos, entre los que está el cubo, cumplen el Teorema de Euler: Caras + vértices = Aristas + 2.
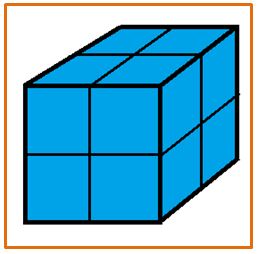
Si al cubo azul de lado L, lo dividimos en cubos iguales de lado L/2 Podemos observar que los cubitos de los vértices del cubo de lado L tienen tres caras pintadas y no aparecerá ningún cubo de lado L/2 con alguna de sus caras pintadas.
Luego tendremos ocho cubitos de lado L/2 con tres caras pintadas, y ninguno con una, dos, o cero caras pintadas.
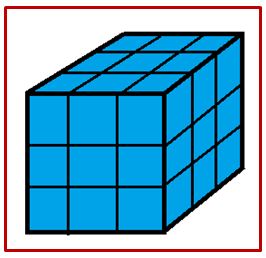
Si al cubo azul de lado L lo dividimos en cubos iguales de lado L/3 obtendremos veintisiete cubitos. Entonces podemos observar que los cubitos de los vértices del cubo de lado L tendrán tres caras pintadas t como hay ocho vértices serán ocho cubitos; los cubitos que están en cualquiera de las doce aristas del cubo grande, pero no en su vértice tienen dos caras azules, como hay uno por arista (12·1=12), los cubitos que están en cualquiera de las seis caras y no tocan ni vértices ni aristas del cubo tienen una cara pintada y como hay uno por cara (6·1=6) y queda dentro un cubo con ninguna cara pintada. Así de los 6 cubitos habrá:
8 con tres caras azules, 12 con dos caras azules, 6 con una cara azul, 1 sin ninguna cara pintada.
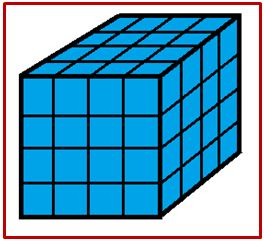
Si al cubo azul de lado L lo dividimos en cubos iguales de lado L/4 obtendremos sesenta y cuatro cubitos. Entonces podemos observar que los cubitos de los vértices del cubo de lado L tendrán tres caras pintadas, por tanto habrá ocho cubitos; los cubitos que están en cualquiera de las doce aristas del cubo grande, pero no en su vértice tienen dos caras azules, como hay dos por arista, habrá 24 (12·2=24), los cubitos que están en cualquiera de las seis caras del cubo y no tocan ni vértice ni arista tienen una cara pintada y como hay cuatro por cara habrá 24 (6·4 = 24) y queda en la parte central del cubo un cubo formado por ocho cubitos sin ninguna cara pintada. Así de los 64 cubitos habrá:
24 con una cara azul, 24 con dos caras azules, 8 con tres caras azules, 8 sin ninguna cara pintada.
Es fácil concluir que si dividimos el lado del cubo en n partes obtendremos como se indica en las figuras anteriores se obtienen n3 cubitos de lado L/n con las siguientes características:
- 8 cubitos con tres caras pintadas (los de los vértices del cubo de lado L)
- 12 (n-2) cubitos con dos caras pintadas (situados en las aristas del cubo de lado L, que no sean vértices)
- 6 (n-2)2 cubitos con una cara pintada (situados en el centro de cada cara que no tocan vértice ni arista del cubo de lado L)
- Finalmente quedan (n-2)3 cubitos con las caras sin pintar situado dentro del cubo y lado (n-2)·L/n.




