René Descartes (1596-1609), en la Primera Parte del Discurso del Método, dio su opinión sobre la Geometría de Euclides. La colocó en la cima del pensamiento humano, y le sorprendió que, con la solidez de sus principios, no se hubiera construido algo más destacado. Afirmaba que el principal resultado que podía lograrse de la Geometría clásica era el puramente formativo del cultivo nuestro espíritu.
Por otra parte, estaba convencido de su Método y recomendaba que, para formar un hábito investigador, era conveniente estudiar primero las cuestiones más fáciles que se presenten a nuestro entendimiento como ideas claras y distintas y luego pasar a los temas más complejos.Con estos supuestos pendaba que su Método no podía estar formado por una lista de fórmulas rígidas aplicables de forma mecánica, semejante al método geométrico. Criticaba tanto a los antiguos, que eran los geómetras euclidianos, como a los modernos, que eran los algebristas que venían pidiendo paso desde el siglo IX con Al-Khwarizmi. Descartes opinaba sobre ellos diciendo:
el análisis de los antiguos está tan circunscrito al análisis de las figuras que no permiten ejercitar el entendimiento sin fatigar en exceso la imaginación. El Álgebra de los modernos está tan sometida a ciertas reglas y cifras que se ha convertido en un arte confuso y oscuro capaz de distorsionar el ingenio.
Descartes llegó a la Geometría Analítica intentando vincular la Geometría de los Elementos de Euclides con el Álgebra para poder aplicarlas mejor en los casos que conviniera. Para ello buscó lo que le parecieron las ideas y relaciones más simple, claras y elementales que se podían dar entre las líneas geométricas que se pudieran expresar con números de la forma más breve que fuera posible. Para ello buscó construcciones geométricas que se correspondieran con la suma, la resta, el producto, el cociente y la raíz cuadrada. Con ese punto de partida pensaba que se relacionaría lo mejor de la Geometría y lo mejor del Álgebra, corrigiendo mutuamente los defectos de una con los procedimientos de la otra.
Esta idea se le ocurrió mientras estuvo en Alemania (como señala Parte Segundo del Discurso) donde debió entrar en contacto con algunos algebristas alemanes, completando y mejorando la notación algebraica que ya conocía el filósofo francés heredada de su compatriota F. Vieta (1540-1603)
El Libro Primero de la Geometría (1637) de R. Descartes lo dedicó a la geometría plana y el autor concretó más diciendo: Sobre los problemas que pueden construirse empleando solamente circunferencias y líneas rectas. Es decir, el libro se iba a ocupar de los antiguos problemas de la Geometría Griega que se resolvían mediante construcciones que se realizaban mediante el uso de la regla y el compás.
Con el uso de la regla y el compás no se cubrían todos los problemas de la geometría plana, ni tampoco podían dibujarse todas las curvas geométricas planas. Descartes conocía los trabajos de algunos geómetras griegos que habían estudiado curvas que no podían dibujarse con regla y compás. Sabía que Apolonio de Perga (262-190 a. de C.) había estudiado las cónicas (elipse, la parábola o la hipérbola) y sabía que otros matemáticos habían definido otras curvas, que ellos llamaron mecánicas, que tampoco podían dibujarse con la regla y el compás, como la Cisoide de Diocles (s. III a. de C.), la Concoide de Nicomedes (280-210 a. de C.) o la Cuadratriz de Dinóstrato (390-320 a. de C). Pero Descartes dejaría el estudio de las curvas más generales para el Libro Segundo de su Geometría, ya que quería partir de los problemas más sencillos y llegar a los más generales.
Los problemas del Libro Primero se reducían a resolver ecuaciones de primer y segundo grado. La razón era que la regla permitía trazar rectas, que responden a ecuaciones de primer grado ax + by + c = 0 y que con el compás se dibujaban circunferencias cuya ecuación era de segundo grado x2 + y2 + Ax + By + C = 0. Por lo tanto, resolver un problema de geometría plana de regla y compás se reducía a resolver problemas de intersecciones de recta con recta, de dos circunferencias entre sí o de una recta con una circunferencia. En resumen resolver problemas geométricos de regla y compás se reduce a resolver en álgebra ecuaciones de primer y segundo grado.
Descartes concibió la idea de que todos los problemas en Geometría podían plantearse y llegar a reducirse de tal forma que para resolverlos no fuera necesario más que conocer la longitud de algunas líneas y que, del mismo modo que en Aritmética, para resolver cualquier problema bastaba con conocer cinco operaciones: suma, resta, producto, cociente y extracción de raíces, las mismas operaciones se podían hacer en forma geométrica.
Partiendo de un segmento rectilíneo, que se tomaba como unidad, y teniendo otros dos segmentos de longitud conocida se puede encontrar un cuarto segmento que sea suma, resta producto o cociente de los dos o raíz de uno de ellos.
La suma y la resta es trivial. Para las demás operaciones:
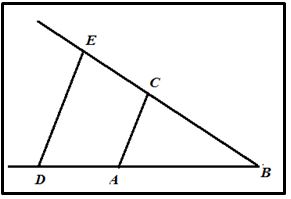
Cálculo de producto:
Si el segmento AB es la unidad y se quiere multiplicar BD por BC, uniendo los puntos A y C y trazando DE paralela a AC, BE es el resultado de la multiplicación, ya que:
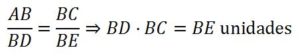
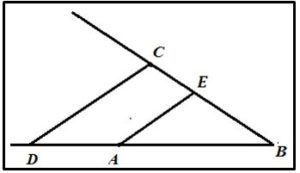
Cálculo del cociente: Si se quiere dividir BC entre BD, uniendo los puntos D y C trazando AE paralela a DC, entonces BE es el cociente de la división
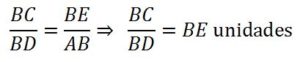
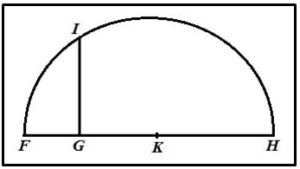
Cálculo de la raíz cuadrada: Para calcular la raíz cuadrada de GH se le añade FG que es la unidad. Haciendo centro en K, punto medio de FH, se traza la semicircunferencia FIH. La perpendicular a FH por el punto G corta a la semicircunferencia en el punto I, GI es la raíz cuadrada de GH
Descartes decía que no era preciso hacer esas constricciones, bastaba con designar a cada una de ellas con una letra. Y a para sumar dos se escribirá a + b, la resta a – b, el producto a·b, el producto de un número por si mismo a2, etc.
Debe observarse que con a2, b3 y expresiones similares eran para Descartes líneas simples y que no se referían a áreas o volúmenes, aunque las nombrara con cuadrados o cubos porque se servía de las expresiones el álgebra, con esta matera de definir operaciones con líneas que daban resultados líneas, se rompía con el principio de homogeneidad dimensional que hacía necesario dotar a los números de dimensión. Si no la expresión: A3 + 2A2 = 6 , se entendería
A3 sólido + 2A2 sólido (por lo tanto, 2 lineal) igual a 6 sólido
Los procedimientos para acceder a las ecuaciones que sirven para resolver los problemas de geometría serían:
Si deseamos resolver un problema inicialmente debe suponerse efectuada la solución, dando nombre a todas las líneas necesarias para su construcción, tanto a las que son conocidas como la las desconocidas. A continuación sin establecer distinción entre las líneas conocidas y las desconocidas debemos descifrar el problema siguiendo el orden que muestre de modos más natural les relaciones entre estas líneas, hasta que se identifique un medio de expresar una misna cantidad de dos forma, esto es lo que se entiende por una ecuación, pues los términos de una de las expresiones son iguales a los de la otra. Deben hallarse tantas ecuaciones como líneas desconocidas se han supuesto [problema de terminado]. … Si existen varias líneas desconocidas es preciso servirse por orden de cada una de las ecuaciones restantes, bien sea considerándolas aisladamente, bien cada una en comparación con las otras, para obtener el valor de cada una de las líneas desconocida. Debe procederse así hasta que no sólo quede una línea desconocida igual a una línea conocida o cuyo cuadrado, cubo… sea igual a a la suma o diferencia de dos o más cantidades una de las cuales sea conocida y las otras estén compuestas de algunas medias proporcionales, cuadrado, cubo, etc, multiplicado por otras cantidades conicidad. Esto los expreso en la forma siguiente:
z=b, z2 = –az + b2, z3 = az2 + b2z – c3, z4 = az3 – b3z + d3, etc.
Es decir z, la cantidad desconocida, es igual a b o el cuadrado de z es igual al cuadrado de b menos a multiplicado por z, o el cubo de z …”
Vieta había designado con consonantes a los parámetros y con vocales a las incógnitas Descartes denotaba los parámetros con las primeras letras del alfabeto y a las incógnitas con las últimas.
Si el problema puede ser resuelto mediante la geometría ordinaria en el plano con rectas y circunferencias, cuando la ecuación haya sido resuelta no encontraremos más que un cuadrado desconocido igual al resultado de multiplicar su raíz cuadrada por alguna cantidad conocida y sumada alguna otra cantidad conocida.
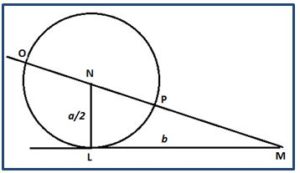
Caso 1: Para resolver la ecuación: x2 = ax + b2
Construir un triángulo rectángulo NLM, de lado LM = b
Y el otro cateto LN =a/2. Prolongando MN hasta O, de modo que NO sea igual a NL x = MO es la solución,
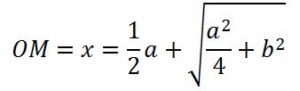
Una versión, en otras geometrías, se resuelve por la potencia de un punto respecto a una circunferencia ya que MO·MP = b2, haciendo MO = x, entonces MP= x – a y sustituyendo en (1), se obtiene:
x·(x – a) = x2 – ax = b2 y, por tanto, x2 = ax + b2 (Libro III de Elementos de Euclides prop 36)
Caso 2: Para resolver x2 = – ax + b2
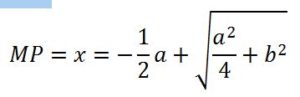
x = MP es la solución, ya que MO·MP = b2 haciendo MP = x, entonces MO= x + a y sustituyendo en (2), se obtiene: x·(x + a) = x2 + ax = b2 y, por tanto, x2 = – ax + b2
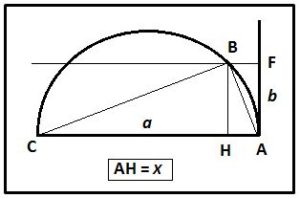
Caso 3: Para resolver x2 = ax – b2. En una semicircunferencia de diámetro AC = a . Levantamos en A una perpendicular a AC y, sobre ella tomamos una distancia AF = b. Por F trazamos una paralela a AC que puede cortar a la semicircunferencia en dos puntos, uno o ninguno. Llamando x = AH, se cumple que BH2 = HA · HC. Llamando HA = x, HC = a – x y teniendo en cuenta que BH = b se obtiene que b2 = x·(a – x)
⇒ b2 = a x – x2 ⇒ x2 = a x – b2
