
En el tiempo que medió entre el siglo XVI y el siglo XVIII se produjo un cambio enorme en el lenguaje matemático. En un primer nivel se puede apreciar globalmente el cambio del dominio de los métodos de la geometría a la hegemonía del lenguaje algebraico. Pero en este largo proceso de dos siglos hay matices que merece la pena destacar, en primer lugar, que con el abandono de los métodos de la geometría euclidiana en la que solamente se podían representar segmentos no cabían las soluciones negativas. En segundo lugar, que, con los métodos algebraicos, ecuaciones del mismo tipo proporcionaban soluciones no positivas (negativas y complejas) que o bien no se consideraban como soluciones o no sabían interpretar. En tercer lugar, que, aunque hubo reticencias para aceptar como números las soluciones negativas y complejas, a finales del siglo XVIII ya se aceptaban como números e incluso como coeficientes (parámetros) de las ecuaciones. Como lo prueba la expresión del Teorema Fundamental del Algebra (TFA) demostrado en 1799 por K.F. Gauss (1777-1855) que dice: Todo polinomio de coeficientes reales o complejos, tiene por lo menos una raíz, real o compleja. O, equivalentemente, que toda ecuación algebraica de grado n con coeficientes reales o complejos tiene n tiene n raíces. Con el manejo de ecuaciones, la aceptación de diferentes clases de números y su representación literal con las mismas operaciones y, por tanto, las mismas propiedades que el resto de los números, dotó al álgebra de un lenguaje cada vez más abstracto, con raíces en la geometría, pero cada vez más alejado de su lenguaje tradicional y sus representaciones.
En lo que sigue tratare se destacar, con ejemplos concretos, algunas “fotos fijas” que señalan los peldaños temporales que superaron los métodos algebraicos de la resolución de ecuaciones.

En las facultades de filosofía de las universidades medievales se estudió el Álgebra Geométrica de Euclides y se utilizó para resolver ecuaciones de segundo grado. El aragonés P. Sánchez Ciruelo (1470-1548), profesor de teología y astronomía en las universidades de París, Alcalá y Salamanca, publicó en 1516 la obra enciclopédica Cursus quattuor Mathematicarum Artium Liberalium (Quadrivium: aritmética, astronomía, geometría y música), en la que recopiló los métodos de la geometría euclidiana, la numeración indo-arábiga, el álgebra de los matemáticos musulmanes y tópicos de otros autores europeos como J. Sacrobosco (1195–1256), L. de Pisa (1175-1240) o Th. Bradwardine (1290–1349) la obra incluía un capítulo dedicado a la resolución de ecuaciones de segundo grado con métodos de la geometría de Euclides.
El Libro II de los Elementos tenía una serie de proposiciones que permitían resolver ecuaciones de segundo grado o, por lo menos, calcular las soluciones positivas de la ecuación. Tomaremos el siguiente ejemplo de una ecuación que se resolvía aplicando la proposición quinta del libro II
Proposición 5: Si se divide un segmento en partes iguales y desiguales mediante dos puntos M y D, el rectángulo determinado por las partes desiguales, más el cuadrado de lado la distancia entre los dos puntos que dividen la recta es igual al cuadrado de la mitad de la recta dada.
Algebraicamente la podemos escribir de la siguiente forma: si tenemos un segmento AB y un punto D divide a AB en dos segmentos desiguales AD = p y DB = q y que otro punto M divide a AB en dos partes iguales, que tendrán la longitud AM = MB = (p+q)/2. Luego la Proposición 5 se puede escribir de forma algebraica de la forma siguiente:
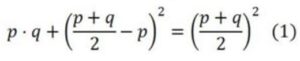
Cuya validez se puede comprobar de forma algebraica y la emplearemos para resolver la ecuación:
(b – x)·x = c2.
Sean AB un segmento de longitud b, M el punto medio de AB y D un punto arbitrario entre A y B, entonces la proposición se puede escribir en la forma:
AD·DB + MD2 = M B2 (2)
Como MB = b/2, llamando a DB = x, entonces MD = (b/2) – x y (2) se transforma en:
(b – x)x + (b/2 – x)2 = (b/2)2
Y como queremos resolver (b – x)·x = c2 quedará:
c2 + (b/2 – x)2 = (b/2)2
Por lo tanto (b/2 – x)2 = (b/2)2 – c2 y haciendo la raíz cuadrada de ambos miembros:
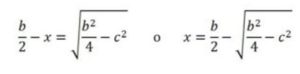
No obstante, la expresión algebraica de la Proposición 5 [c2 + (b/2 – x)2 = (b/2)2 ] nos permite apreciar el modo en que se usaba la proposición para resolver este tipo de ecuaciones cuadráticas mediante una construcción geométrica, ya que nos indica que la figura geométrica que debemos construir es un triángulo rectángulo de catetos:
c y b/2 – x y de hipotenusa b/2.
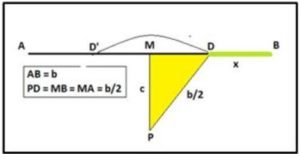
Para resolver geométricamente la ecuación
c2 + (b/2 – x)2 = (b/2)2
trazamos un segmento AB de longitud igual a b y sobre su punto medio M levantamos una perpendicular MP de longitud igual a c. Con centro en el punto P y radio b/2 trazamos una circunferencia que corta al segmento AB en los puntos D y D’: El segmento DB = AD = x es la solución de la ecuación propuesta. Es evidente que:
Si b/2 > c o, equivalentemente b > 2c , la ecuación tiene dos soluciones, porque la circunferencia de centro P y radio PD corta a AB en dos puntos
Si b/2 < c o, equivalentemente b < 2c, la ecuación no tiene solución, porque la circunferencia de centro P y radio PD no corta a AB
Si b/2 = c o, equivalentemente, b = 2c la ecuación tiene una sola solución x = b/2.
En la edad media se abordó la resolución de ecuaciones por representación geométrica; se utilizó el método de completar cuadrados y unas representaciones más fáciles de visualizar. Un ejemplo:
more geométrico fue el empleado por Al-Kwarizmi (780-850) con este ejemplo:
Resolver la ecuación: x2 + 6x = 7 para lo que realizó la siguiente descomposición del cuadrado:
x2 + 6x = 7 ⇒ (x + 3 )2 = x2 + 6x + 9 = 7 + 9 = 16 ⇒
⇒ (x + 3 )2 = 16 x + 3 = 4 Þ x = 1
Observemos que con los procedimientos de la geometría euclidiana no pueden descubrirse las soluciones negativas, en este caso, con el método señalado no se puede calcular la solución x = -7
Un escalón diferente en la resolución de ecuaciones fue la fase del algebra retórica por el libro de G. Cardano (1501-1576) Ars Magna (El gran arte o las reglas del álgebra), considerado como el texto precursor del álgebra moderna. Los métodos para la resolución de ecuaciones expuestos por Cardano, aunque se sustentan en el razonamiento geométrico, están expresados en el lenguaje cotidiano. Puede verse más ampliamente en:
http://vicmat.com/las-reglas-cardano-resolver-la-ecuacion-segundo-grado/
Donde se explica la resolución de los diferentes tipos de ecuaciones, atendiendo a las ecuaciones con coeficientes positivos, que los denominaba así:
Primero: Squeaxno: (cuadrado (Squ), igual a (e) primera potencia (ax) y constante (no)):
x2 = ax +N.
Cardano daba la siguiente regla de resolución: Suma el cuadrado de la mitad del coeficiente de la primera potencia con la constante de la ecuación y calcula la raíz cuadrada del total. A esto se le suma la mitad del coeficiente de la primera potencia y la suma da el valor de x.
Segundo: Noesquax: (constante (No) igual a (e) cuadrado (squ), primera potencia (ax) )
N = x2 + ax
Cardano daba la siguiente regla de resolución: Suma el cuadrado de la mitad del coeficiente de la primera potencia con la constante de la ecuación y calcula la raíz cuadrada del total. A esto se le resta la mitad del coeficiente de la primera potencia y el resultado es el valor de x.
Tercero: Axesquno: (primera potencia (ax) igual a (e) cuadrado (squ) y constante (No) )
ax = x2 + N
Cardano daba la siguiente regla de resolución: Al cuadrado de la mitad del coeficiente de la primera potencia se le resta la constante de la ecuación y calcula la raíz cuadrada del total. A esto se le resta a la mitad del coeficiente de la primera potencia o se le suma y el resultado es el valor de x.
Un escalón diferente y decisivo en la resolución de ecuaciones fue la fase del algebra literal, representada F.Vieta (1540-1603) y por la obra In artem analyticam isagoge (1591), en la cual introdujo notación que hacía uso de letras en las fórmulas algebraicas, para resolver la ecuación:

ax2 + bx + c = 0,
haciendo el cambio de variable: x = y + z obtenemos:
a(y + z)2+ b(y+z) + c = 0 ⇒ ay2+ (2az+b)y + az2+ bz+c = 0
calculamos z para que se anule el término de primer grado en y:
(2az + b) = 0 ⇒ z = – b/2a
Sustituyendo:
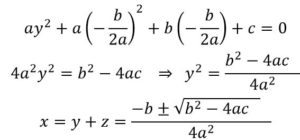
La introducción de la notación simbólica asociada a Viète (1540-1603), marca el inicio de una nueva etapa en la cual R. Descartes (1596-1650) contribuyó de forma importante a la difusión de dicha notación. En este momento, el álgebra se convierte en la ciencia de los cálculos simbólicos y de las ecuaciones. Posteriormente, Euler (1707-1783) la definió como la teoría de los cálculos con cantidades de distintas clases (refiriéndose a números negativos, racionales, radicales y complejos) estudio de progresiones, logaritmos, etc.
Una vez aceptados los diferentes números como soluciones y coeficientes de las ecuaciones se formuló el teorema fundamental del algebra (TFA) que dice:
Todo polinomio de coeficientes reales o complejos, tiene por lo menos una raíz, real o compleja”.
El teorema fundamental del algebra era conocido desde tiempos muy antiguos y su evidencia, que procedía de muchos ejemplos, era tan fuerte, que incluso fue usado antes de ser demostrado. En 1746 J. le Rond d’Alembert (1717-1783) lo probó por primera vez, aunque su demostración no era muy rigurosa, y fue muy criticada, pero la idea de D’Alembert fue utilizada por K. Weierstrass (1815-1897), que la desarrollo con más de rigor. La primera prueba realmente satisfactoria fue realizada por K. F. Gauss (1777-1855 en 1799. Este gran matemático hizo otras tres pruebas, la última, puramente de existencia, en 1849.
El lenguaje algebraico se hizo todavía más abstracto cuando se buscaron fórmulas de resolución de ecuaciones algebraicas por radicales y abrió campos de investigación nuevos que serían el origen de la teoría de grupos. Pero ese tema lo dejaremos para una segunda parte.
Víctor Arenzana Hernández




