En este artículo se van a analizar algunas propiedades de los cuadriláteros. Es decir, los trapezoides, que, según geometría elemental son los cuadriláteros convexos sin lados paralelos. Y, más particularmente, estudiaremos los cuadriláteros inscriptibles.
Proposición 1.- Los puntos medios de los lados de un cuadrilátero son los vértices de un paralelogramo.
Demostración: (según la figura). Si ABCD es un cuadrilátero. Sea M es el punto medio de AB, N es el punto medio de BC, P es el punto medio de CD y Q es el punto medio de DC.
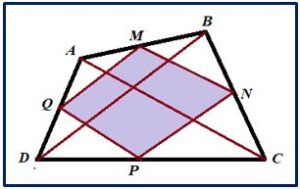
El segmento QM es la paralela media del triángulo ABD por lo tanto será paralela a la diagonal BD y PN es la paralela media del triángulo BCD por lo tanto será paralela a la diagonal BD. Por lo que se deduce que QM y PN son iguales y paralelas. El mismo razonamiento vale par QM y PN. Por lo tanto, MNPQ es un romboide cuyos lados miden la mitad que las diagonales a las que son paralelos.
Proposición 2.- La superficie del romboide MNPQ es la mitad de la superficie del cuadrilátero ABCD:
Demostración:
Area ABD = 4 Area AMQ
Area BCD = 4 Area NCP
Area ACD = 4 Area QPD
Area ABC = 4 Area BNM
Sumando miembro a miembro se obtiene: (Llamamos triángulos blancos a los triángulos de los vértices del cuadrilátero ABCD)
2 (Área del Cuadrilatero) = 4 (Suma de triángulos blancos)
Area del Cuadrilatero = 2 (Suma de triángulos blancos)
(Suma de triángulos blancos) = 1/2 (Area del Cuadrilatero),
Por lo tanto, la superficie del romboide MNPQ es la mitad de la superficie del cuadrilátero ABCD
Proposición 3 (Teorema de Ptolomeo). – En todo cuadrilátero ABCD cíclico (inscriptible en una circunferencia) el producto de las diagonales es igual a la suma de los productos de los lados opuestos.
Esto es: AC · DB = AB · CD + BC · AD.
El recíproco de este teorema también se cumple, es decir, si un cuadrilátero ABCD cumple la rlación siguiente:
AC · DB = AB · CD + BC · AD , entonces es inscriptible en una circunferencia).

Corolario 1.- (El teorema de Ptolomeo implica el teorema de Pitágoras) Si el cuadrilátero es un rectángulo, el Teorema de Ptolomeo sería el Teorema de Pitágoras.
Demostración: Como el rectángulo es un cuadrilátero inscriptible, cumplirá el Teorema de Ptolomeo, por lo tanto, se verificará que: AC · DB = AB · CD + BC · AD.
Como AC = DB, además AB = CD y BC = AD. Por lo tanto, AC2 = AD2 + BC2.

Corolario 2. Dado un triángulo equilátero ABC inscrito en una circunferencia y un punto P de la misma. La suma de las distancias desde P a los vértices más próximos es igual a la distancia desde P al otro vértice.
Demostración: El triángulo equilátero ABC con el punto P forman un cuadrilátero inscriptible ABPC. Aplicando el Teorema de Ptolomeo, se obtiene:
AC·PB + CP·AB = AP·CB
equivalentemente, según indica el dibujo:
a·n + m·a = p·a y,
simplificando la igualdad, obtenemos: n + m = p, que es lo que se quería demostrar
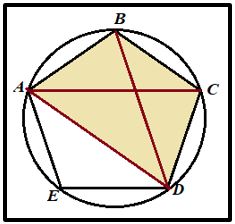
El número áureo El pentágono regular es un polígono inscriptible. Consideremos el pentágono ABCDE y el cuadrilátero ABCD formado por tres lados del pentágono AB = BC = CD = a y la diagonal AD = d. Aplicando el Teorema de Ptolomeo al cuadrilátero ABCD se tiene:
AB·CD + BC·AD = AC·BD, equivalentemente: a·a + a·d = d·d
Dividiendo entre a2 se obtiene la ecuación: 1 + d/a = (d/a)2 , haciendo x = d/a se obtiene la ecuación: x2 – x – 1 = 0
Cuya solución positiva es el número áureo:
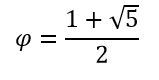
EL TEOREMA DE PTOLOMEO Y LA TRIGONOMETRÍA
Cuando uno de los lados del cuadrilátero inscriptible ABCD es el diámetro de la circunferencia (en el dibujo AD = 2r) el Teorema de Ptolomeo muestra su interpretación trigonométrica. Precisamente por sus consecuencias trigonométricas y por su aplicación a los cálculos de Astronmía, el Teorema de Ptolomeo fue uno de los teoremas más conocidos y utilizados de la Geometría Euclidiana. El teorema fue enunciado y demostrado por primera vez en el Almagesto de Claudio Ptolomeo (c.100-c. 170). El Almagesto fue la obra más importante de la Astronomía antigua y estuvo vigente durante quince siglos. El teorema apareció como una herramienta trigonométrica; al parecer el método se basa, al menos en parte, en los métodos utilizados en las Cuerdas en un círculo del astrónomo Hiparco de Nicea (190-120 a.C.). Las tablas trigonométricas de esa época se calculaban aplicando el Teorema del cual se obtenían fórmulas para calcular la cuerda del arco mitad, de la suma de ángulos.

AC·BD = AD·BC + AB·CD ⇒
⇒ AD·BC = AC·BD – AB·CD ⇒
⇒ 2r·BC = AC·BD – AB·CD,
y dividiendo ambos miembros entre 4r2, obtenemos:
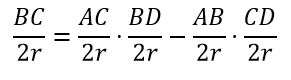
Como el triángulo ABD es rectángulo en B, ABM es rectángulo en B, y ACD es rectángulo en C,
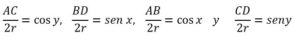
Por otra parte: sen (x-y) = BM/AM (triángulo ABM)
Como el triángulo AMD es semejante al BMC: sen (x-y) = BM/AM = BC/AD = BC/2r.
Y, entonces, sustituyendo en la fórmula anterior se obtiene:
sen (x-y) = sen x· cos y – cos x·sen y
que es la fórmula del seno de la diferencia obtenida a partir del Teorema de Ptolomeo..