DIFERENTES FORMAS DE DESCOMPONER UN NÚMERO EN FACTORES

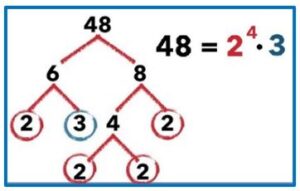
LA DESCOMPOSICIÓN DE UN NÚMERO EN FACTORES PRIMOS ES ÚNICA

La descomposición en factores primos consiste en descomponer cierto número en números primos, llamados factores, cuyo producto tenga como resultado el número original. El teorema fundamental de la aritmética o teorema de factorización única afirma que todo entero positivo mayor que 1 es un número primo o bien un único producto de números primos.

EL NÚMERO DE DIVISORES DE UN NÚMERO

Un número natural o es primo o es compuesto. En caso de que el número sea primo, éste tiene dos únicos divisores que son el 1 y el propio número. Div(7) = {1, 7}

En caso de que el número sea compuesto, siempre tiene algún otro divisor más. De hecho, esto es, una definición de número compuesto. Un número compuesto lo es si tiene más de dos divisores. Pero ¿cuántos divisores tiene este número compuesto?

Consideremos el número 360 = 2³ · 3² · 5¹

El número de divisores será igual al número de sumandos de este producto:

(1+2+2²+2³)·(1+3+3²)·(1+5), es decir, serán 4·3·2 = 24 divisores.

Fácilmente se puede ver que si  n = a^p · b^q · c^r ….

N_D = Nº de divisores de n = (p+1)·(q+1)·(r+1)···

¿DE CUÁNTAS MANERAS SE PUEDE DIVIDIR UN NÚMERO COMPUESTO EN DOS FACTORES?

Tengamos en cuenta que para que un número n = a^p · b^q · c^r … sea cuadrado los exponentes p, q, r…, de su descomposición en factores primos deben ser pares, por tanto:

N_D = Nº de divisores de n = (p+1)·(q+1)·(r+1)··· será impar.

Por otra parte, si n = a^p · b^q · c^r … no es cuadrado, uno, al menos, de los exponentes p, q, r…, de su descomposición en factores primos debe ser impar, por tanto

N_D = Nº de divisores de n = (p+1)·(q+1)·(r+1) ···    será par

DESCOMPONER n COMO PRODUCTO DE DOS FACTORES:

Si el número n no es cuadrado las maneras posibles son:

N_D/2= [(p+1)·(q+1)·(r+1)···(z+1) ]/2

Si n es cuadrado tiene un número impar de divisores, por tanto, tendrá un divisor central Ön el número las maneras posibles son:

(N_D+1)/2= [(p+1)·(q+1)·(r+1)···(z+1) +1 ]/2

¿DE CUÁNTAS MANERAS SE PUEDE DIVIDIR UN NÚMERO COMPUESTO EN DOS FACTORES PRIMOS ENTRE SI?

n = a^p· b^q· c^r· d^s…   m factores primos distintos. Para que n = J·K , siendo J  y  K primos entre si debe cumplirse:

1.   J = a^p y K = b^q c^r· d^s…  o bien   J = pb^q  y  K = a^p· c^r· d^s…  etc

de este tipo hay  C_m,1 = m

1.  Del tipo J = a^p b^q y K = c^r· d^s… de estos hay  C_m,2 = m(m-1)/2

Siguiendo sucesivamente con los J que tienen tres factores primos distintos y K el resto  de factores, el número de formas de descomponer un número compuesto en producto de dos factores primos entre si será:

½[C _m,1 + C _m,2 + C _m,3 + … + C _m,m-1 + C _m,m] = ½ [(1+1)^m]= 1/2( 2^m)  = 2^m-1

Ejercicio1: ¿Cuántos divisores tiene 105? Sol: 8. Incluido 1 y 105

Ejercicio2: ¿Cuántos divisores tiene 180? Sol 30. Incluido 1 y 280

Ejercicio 3: ¿De cuántas formas se puede descomponer 180 en producto de dos factores? Sol: 9

Ejercicio 4: ¿Cuántos divisores tiene 225? Sol 9: Incluido 1 y 225

Ejercicio 5: ¿De cuantas formas se puede descomponer 225 en producto de dos factores?  Sol 5