La Teoría de la Relatividad aporta una visión del tiempo algo diferente de la habitual. Una situación paradójica de la visión relativista del tiempo es la paradoja de los gemelos, que se puede exponer de la siguiente forma: Consideremos a dos hermanos gemelos, uno de ellos hace un viaje en un módulo espacial a una velocidad próxima a la de la luz mientras que el otro se queda en Tierra. Cuando regresa el astronauta es más joven que el que ha permanecido en la Tierra. Es decir, que el tiempo pasa más despacio para el gemelo astronauta que para el que permaneció en la Tierra y, por tanto, envejece más despacio.
La Teoría también afirma que si tomamos el punto de vista del astronauta el gemelo de la Tierra sería el que le parecería más joven. ¿Cuál es la solución a esta paradoja?
El primer párrafo del artículo de Einstein Sobre la electrodinámica de los cuerpos en movimiento (1905), donde Einstein formuló los postulados de la relatividad especial, comienza con unas disquisiciones sobre el movimiento absoluto y el movimiento relativo:
La electrodinámica de Maxwell conduce a asimetrías en su aplicación a os cuerpos en movimiento. Piénsese en la interacción electrodinámica entre un imán y un conductor. El fenómeno observable sólo depende del movimiento relativo de conductor e imán, mientras que en la concepción habitual se distinguen dos casos según quien consideremos que se mueva respecto a otro. Concretamente, si se mueve el imán y permanece quieto el conductor aparece en torno al imán un campo eléctrico de cierto valor de energía que genera una corriente en los lugares en los que se encuentran partes del conductor.
Si embargo, si se mantiene en reposo el imán y se mueve el conductor en torno al imán no surge campo eléctrico alguno y si en cambio en el conductor una fuerza electromotriz a la cual no corresponde ninguna energía intrínseca, pero que-suponiendo la igualdad de movimiento relativo en ambos casos considerados-da lugar a corriente eléctricas de la misma intensidad y dependencia temporal que las fuerzas eléctricas del primer caso.
Ejemplos similares junto con los intentos no coronados por el éxito de descubrir algún movimiento de la Tierra con relación al medio luminoso (se refiere al experimento de Michelson y Morley), llevan a la suposición de que el concepto de espacio absoluto no se corresponde con ninguna de las propiedades de los fenómenos que se producen en la mecánica y ni con los fenómenos de la electrodinámica. Apuntan más en la dirección de que las leyes de la electrodinámica y de la óptica son válidas en todos los sistemas de referencia para los que son ciertas las ecuaciones de la mecánica (es decir, los sistemas de referencia inerciales).
Aceptaremos esta hipótesis (cuyo contenido llamaremos desde ahora Principio de relatividad) a la categoría de postulado, e introduzcamos además otro, cuya incompatibilidad con el primero es sólo aparente, a saber: que la luz se propaga siempre en el vacío a una velocidad c independiente del estado del movimiento del cuerpo emisor. Estos dos postulados bastan para obtener una teoría electrodinámica de cuerpos en movimiento simple y sin contradicciones…”.
Estos son los dos postulados de la Relatividad Especial:
- Las leyes fundamentales de toda la física (de la mecánica y del electromagnetismo) se escriben igual en cualquier sistema de referencia inercial (Principio de relatividad)
- La luz se propaga en el vacío con una velocidad c independiente del posible movimiento de la fuente emisora o del estado de movimiento del observador.
En el párrafo siguiente del artículo citado Einstein habla de Sistemas de Referencia Inerciales entre los que se podían aplicar las transformaciones de Galileo y dice que cuando queremos describir el movimiento de un punto material, expresamos sus coordenadas en función del tiempo y dice: No hemos de perder de vista que una descripción matemática de ese tipo sólo tiene sentido físico si está previamente clarificado lo que se entiende por tiempo.
Partimos de la base de que todos los procesos físicos en los que juega papel el tiempo son sólo criterios sobre sucesos simultáneos. Todas las dificultades sobre simultaneidad podrían vencerse si en todos los lugares se conociera la hora de mi reloj (tiempo para el lugar en que se encuentra el reloj en ese momento) pero eso no es tan simple cuando se trata de relacionar temporalmente series de sucesos diferentes, es decir, de medir el tiempo en sucesos que tienen lugar en lugares alejados de mi reloj. Así, podemos hablar del tiempo en A y tiempo en B
El tiempo en A y en B sólo se pueden relacionar si el tiempo que precisa la luz para ir de A a B es el mismo que el de B a A. Así la luz va de A en el instante tA a B en el instante tB y vuelve a A instante t’A. Así:
(A, tA) → (B, tB) → (A,t’A) tA – tB = tB – t’A
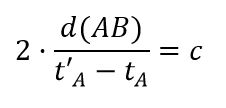
Por el segundo postulado de la relatividad de Einstein, la velocidad de la luz, c, es constante para cualquier observador en cualquier sistema de referencia, esta característica de la luz da lugar a una nueva forma de medir el tiempo y permite diseñar un reloj para poner de manifiesto que el tiempo es relativo en el sentido de que depende del observador. En la Teoría de Relatividad se suele utilizar el llamado reloj de luz.
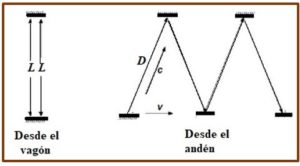
El reloj de luz consiste en un rayo de luz, emitido desde la base inferior de un tubo cilíndrico, que se refleja en un espejo situado en la base superior y que vuelve a reflejarse en el espejo la base inferior. Si la distancia entre el suelo y el techo es L, la unidad de tiempo de ese reloj es el tiempo que utiliza la luz en una ida y vuelta, es decir, la unidad de tiempo para un observador en ese vagón será: 2L /c.
Por ejemplo, si L = 1,5 m, la unidad de tiempo de ese reloj será 3m/300.000km/s = 10-8 s = 0,01 μs (micro segundos,). Con estos relojes mediremos el tiempo en relatividad.
MEDIDA DEL TIEMPO EN RELATIVIDAD. Planteemos el siguiente experimento mental. Desde un andén de la estación un observador A está en un vagón de altura L y mide el tiempo con un reloj de luz que consiste en un rayo luminoso que parte del suelo, se refleja en el techo y después de haber recorrido 2L metros vuelve a reflejarse. La unidad de tiempo de ese reloj, para el observador A, será en 2L/c = t (tA segundos), que es el tiempo que emplea en una oscilación,
Medirá el tiempo propio del vagon que es una magnitud fundamental en relatividad que se define como el tiempo que mide un reloj unido a un objeto en movimiento; es una propiedad absoluta del movimiento del objeto, y por tanto, del reloj en ese movimiento.
Para este reloj, la salida del destello y su llegada ocurren en un mismo punto del sistema. Llamaremos a este tiempo, tiempo propio del reloj.
En este caso la salida del destello y su llegada ocurren en dos lugares diferentes del espacio. Por eso decimos que el tiempo medido con el reloj fijo a nuestro laboratorio es un tiempo impropio.
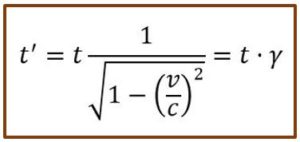
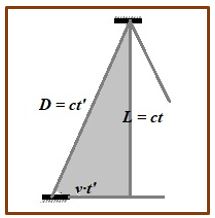
Si el tren se mueve con movimiento rectilíneo y uniforme con una velocidad v, para el observador A el reloj de luz no habrá cambiado, nada, pero un observador B, situado en el andén, reparará que la luz habrá recorrido una distancia D > L, y, como la velocidad de la luz es independiente del sistema de referencia en que se observe, la distancia, D > L que observa lo habrá recorrido en un tiempo t’ > t. Estas distancias están conectadas por la siguiente relación geométrica:
![]()
De dónde:
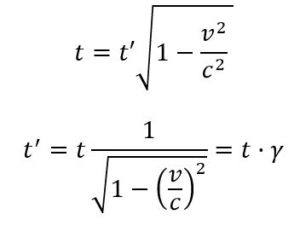
Donde se observa que, dado que, por el principio de relatividad la velocidad c del rayo luminoso es invariante, v < c, γ > 1 son constantes. el tiempo se ha tenido que dilatar. Las mediciones de tiempo no son iguales en sistemas de referencia en movimiento relativo. Por esa razón, el tiempo del vagón pasa más lento para el observador el andén.




