La palabra duelo tiene varias acepciones: una proviene del latín dolus que significa aflicción, dolor o sentimiento, pero si atendemos a otro significado parece que tiene su origen el vocablo latino duellum que estaba compuesto por la fusión de dos palabras duo (dos) y bellum (guerra, contienda), de dónde le se le atribuye el significado de combate entre dos personas o dos grupos. En este escrito se presentan dos problemas de probabilidades sobre los resultados de los enfrentamientos entre en dos personas y entre tres. El primer caso, entre dos personar sería, evidentemente un duelo, el segundo entre tres, no sería un duelo propiamente, de ahí, el licencioso vocablo “trielo” que quiere reflejar esta situación
Problema 1: Dos jugadores A y B igualmente hábiles juegan a cara o cruz. El juego consiste en lanzar la moneda una vez cada uno. El jugador A gana si en su lanzamiento sale cara (C) y B gana si sale cruz (X). Sortean quien comienza a jugar y comienza A ¿Cuál será la probabilidad de ganar de cada uno de ellos?
Solución: A gana en un lanzamiento si sale C. Gana en tres lanzamientos si sales CXC, Gana en cinco lanzamientos si sale CXCXC, en siete si sale: CXCXCXC,
Los sucesos C y X son independientes y P (C) = P(X) = 1/2. Entonces:
P (Gane A) = P (C) + P (XCC) + P (XCXCC) + P (XCXCXCC) + … =

El jugador B gana en dos lanzamientos si sale XX. Gana en cuatro lanzamientos si sales XCXX, Gana en seis lanzamientos si sale XCXCXX,… luego
P(Gane B) = P (XX) + P (XCXX) + P (XCXCXX) + … =
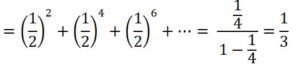
Los que muestra que el que comienza a jugar, A, tiene doble probabilidad de ganar que B
Problema 2: Tres señores A y B y C dirimen sus diferencias como en las películas del oeste, en un duelo, las probabilidades de acierto de cada uno de ellos son, respectivamente, 1, 0,8 y 0,5. Las reglas del duelo consisten en hacer un disparo cada vez, por orden, hasta que quede un solo superviviente. Cada uno puede elegir libremente sobre quien disparar. ¿Cuál será la probabilidad de sobrevivir para A, B y C si cada uno de ellos actúa de una forma óptima para su supervivencia?
Solución:
La estrategia óptima de A será disparar sobre B. Así tendrá una probabilidad de 0,5 de seguir vivo. Si disipara sobre C, quedaría vivo B y solamente tendría una probabilidad de 0,20 de sobrevivir.
La estrategia óptima de B es disparar a A, porque, si no, en el siguiente turno, A, que no falla, lo matará.
La estrategia de óptima de C, que sabe que A y B tienen mejor puntería que él, consistirá en disparar al aire mientras sus dos oponentes estén vivos, ya que A y B se enzarzarán en un duelo particular para matarse el uno al otro para eliminar peligros mayores. Esta estrategia le permitirá a C disparar contra el superviviente en primer lugar.
Con estas premisas: Consideraremos primero el duelo partícular entre A y B, ya que, mientras vivan los dos, C no intervendrá, disparando contra el superviviente.
DUELO ENTRE A y B
Probabilidad de que sobreviva A: A tiene una probabilidad de 0,5 de que le toque disparar antes que B (con probabilidad 1 de matar a B), y, en este caso, tiene una probabilidad de 0,5 de sobrevivir. Pero también puede sobrevivir disparando en segundo lugar (para lo que tiene probabilidad 0,5) , si dispara B y falla (probabilidad 0,2), luego
Probabilidad (A sobreviva en el duelo entre A y B ) = 0,5·1 + 0,5·0,2 = 0,6
Pero A, después de vencer a B, tiene que enfrentarse con C con el que tiene una probabilidad de 0,5 de sobrevivir. Luego la probabilidad de que sobreviva al duelo con B y con C será:
Probabilidad [A sobreviva al duelo y a C) = 0,6·0,5 = 0,30
Probabilidad de que Sobreviva B:
La probabilidad de sobrevivir B frente a A es (que dispare en primer lugar (0,5) y que después no falle (0,8), es decir: B tiene una probabilidad de sobrevivir al duelo con A de 0,5·0,8 = 0,4, pero también puede sobrevivir en su suyo con C si se sigue una sucesión de fallos alternativos lo que da una probabilidad de sobrevivir de:

0,5 · 0,8 + 0,5·0,2·0,5·0,8 + 0,5·0,2·0,5·0,2·0,5·0,8 + …. =
0,5 · 0,8 [ 1 + (0,5·0,2) + (0,5·0,2)2 + (0,5·0,2)3 + (0,5·0,2)4 +
… +… ] = 0.4 [1+ (0,1) + (0,1)2 + (0,1)3 + (0,1)4 +….. + …] =
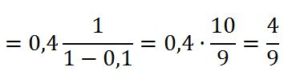
Como la probabilidad de sobrevivir al duelo con A era 0,4 = 2/5. La probabilidad de que B sobreviva a A y a C será el producto de ambas:
![]()
Finalmente, la probabilidad de que C sobreviva a los sus dos contrincantes será:
![]()
De esta forma, C, el jujador menos hábil, con una probabilidad menor de salvarse resulta el más beneficiado por la estrategia óptima del “trielo”.