La Física Aristotélica dividía los lugares donde se producían los fenómenos naturales en dos zonas: Una era el mundo sublunar, donde vivían los hombres, se producían fenómenos meteorológicos y se desarrollaba la vida con nacimientos y muertes; la otra zona era el mundo supralunar poblado de astros que se movían describiendo circunferencias de forma ordenada y eterna. Por otra parte, en los cielos supralunares, en tiempos de Aristóteles (384-322 a. C.), no se habían apreciado cambios de forma ni apariciones de nuevos astros, mientras que el mundo sublunar se caracterizaba por sus incesantes cambios que se denominaron en la Filosofía Griega procesos de generación y corrupción.
En los cielos el único movimiento natural e inalterable que se apreciaba desde la Tierra era el movimiento circular que describían los astros y para Aristóteles en el mundo sublunar el único movimiento natural era el movimiento rectilíneo y vertical dirigido hacia el centro de la Tierra. Este movimiento lo seguían todos los cuerpos para ocupar el lugar que les correspondía por su naturaleza para estar en equilibrio. Los cuerpos con más proporción de los elementos tierra o agua se dirigirían hacia el centro de la Tierra y los que tuvieran mayor cantidad de aire o fuego se elevarían en sentido opuesto.
Aristóteles distinguió, además de los movimientos naturales, otro tipo de movimientos, que llamó movimientos violentos, que eran aquellos en los que sobre el objeto que se movía se ejercía una fuerza o violencia que los hacía separarse de su comportamiento natural, como sucedía cuando se lanzaba una piedra con una honda o en desplazamiento de cualquier proyectil .
La Física del movimiento local de Aristóteles fue analizada y criticada por muchos estudiosos y comentaristas de su obra entre los que se pueden destacar al filósofo bizantino J. Filopón (490-570), al filósofo griego de Simplicius de Cilicia (490-560), y a los filósofos andalusíes Avempace (1080-1139) y Averroes (1126-1198).
Las críticas a la Física Aristotélica se centraban en dos temas, uno era sus conclusiones sobre la caída de los graves y otro la interpretación de la causa los movimientos violentos. Aristóteles mantenía que los cuerpos más pesados llegaban al suelo antes que los más ligeros y aventuró un resultado que decía que la rapidez de los cuerpos en caída libre era proporcional a su peso. Esta creencia no comprobada se mantuvo casi dos milenios y, aunque no se realizaron medidas precisas, los comentaristas de la obra del estagirita la rebatieron con el simple argumento de que una bola de kilogramo dejada caer desde una altura h , no caía cien veces más rápido que una bola de 10 gramos que caía desde la misma altura.
Más difícil era comprender el comportamiento de los movimientos violentos desde los presupuestos de la Física Griega. Para Aristóteles los movimientos naturales se producían impelidos por una fuerza interior que los hacía seguir la vertical y no necesitaban un agente externo que los moviera. Pero los movimientos violentos necesitaban una causa eficiente que actuara en contacto con el objeto móvil. La exigencia de que la causa motriz tuviera que estar necesariamente en contacto con el móvil, era una grave dificultad para explicar el movimiento de los proyectiles, el magnetismo o las mareas. En estos casos la causa eficiente parecía actuar a través de la continuidad del medio en el que se desplazaban. Estas dudas las padeció Ch. Huygens (1629-1695), conocido como el Newton holandés, para aceptar la acción a distancia de la fuerza de gravitación de Newton
Llegados a este punto podemos plantearnos el problema de describir la trayectoria de una bala lanzada por un cañón de artillería. Evidentemente, el proyectil era lanzado en el mundo sublunar y llevaba, según la denominación aristotélica, un movimiento violento en el que la bala no seguía unida a la causa eficiente que la había lanzado, tal y como como exigía la Física de Aristóteles.
Una explicación razonable del movimiento de la bala fue dada en el siglo XIV con la Teoría del Impetu. Teoría que fue defendida por J. Buridan (1300-1361), discípulo de G. de Ockham (1280-1349) en la Universidad de París. Según la Teoría el motor imprimía una fuerza al proyectil que se iba perdiendo poco a poco. En realidad la Teoría era una forma de racionalizar la dinámica de Aristóteles al postular la existencia de una fuerza motriz impresa incorporada al móvil.
La Teoría del Impetu aportó ideas nuevas y contribuyó a iluminar la Teoría de Aristóteles sobre el movimiento local, pero sólo cuestionaba las causas del movimiento y la naturaleza del mismo, pero no se preguntaba cómo era la trayectoria de un proyectil, seguramente, porque no se necesitaba un estudio preciso de la misma. Sin embargo, los artilleros necesitaban conocer las trayectorias de los proyectiles para hacer blanco de forma precisa en los objetivos militares.
Simultáneamente a estas especulaciones filosóficas, en la artillería se empezó a utilizar la pólvora. Probablemente se utilizó por primera vez en 1262, en el cerco de Niebla (Huelva), pero es seguro que se usó en el sitio de Algeciras de 1344 y se empleó masivamente en la Guerra de los Cien Años (1337-1453) entre Inglaterra y Francia.
Poco a poco, la artillería se iba haciendo decisiva en el desarrollo de las guerras. En el sitio de Burdeos de 1452 se utilizaron por primera vez bombas, que eran proyectiles cargados de pólvora que explosionaban en el momento del impacto. El efecto de las bombas era devastador cuando acertaban en el objetivo y, en artillería, fue adquiriendo cada vez más importancia dar en el blanco por lo que se hizo importante conocer la trayectoria del proyectil en lugar de afinar la puntería observando dónde caían los proyectiles y ajustando la posición e inclinación del cañón por el método de ensayo y error.
En los Tratados de Artillería se intentaba determinar la forma de la trayectoria. En 1537, N. Tartaglia (1499-1557) publicó su libro La Nueva ciencia en el que acometió el estudio de las trayectorias de los proyectiles. Propuso que los proyectiles de un cañón debían tener tres tramos: uno recto en el que la bala se movía con movimiento rectilíneo, inclinado y violento, según la terminología aristotélica, otro tramo curvo en el que proyectil se adaptaba, sin cambios bruscos a un tercer tramo que seguía una línea recta vertical dirigida al centro de la Tierra. La hipótesis de Tartaglia de admitir un tramo curvo en la trayectoria de un proyectil era innovadora, porque se creía que en el mundo sublunar solamente existía el movimiento rectilíneo. D. Santbech (¿?-1561), suponía que la trayectoria estaba formada un tramo recto ascendente y otro descendente también recto.
Las ideas de Tartaglia fueron recogidas en el Tratado de Artillería (1613) del artillero español D. Ufano, y supusieron un choque con las ideas aristotélicas, que mantenían que sólo en los cielos podían existir movimientos curvos, pero Tarataglia no se abría a la experimentación ni tampoco a investigar otras posibles trayectorias para los movimientos y seguía apegado a la idea de que el movimiento rectilíneo y el circular eran los únicos posibles en el universo.
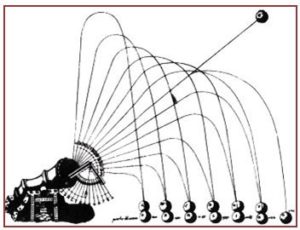
Uno de los grandes descubrimientos científicos de Galileo fue determinar la trayectoria parabólica de los proyectiles a partir de la composición de dos movimientos teóricos, que se suponen independientes entre sí. El pisano elimina del movimiento diferentes cualidades e incluso observaciones visuales, y redujo la naturaleza del movimiento a términos puramente cuantitativos y medibles a los que se les podían aplicar los métodos matemáticos, como lo hizo en su obra Consideraciones y demostraciones sobre dos nuevas ciencias (1638):
«Sabemos que el movimiento que tendrá lugar sobre un plano será uniforme y perpetuo, en el supuesto de que el plano se prolongue hasta el infinito. Si por el contrario, el plano es limitado, el móvil que suponemos dotado de gravedad, una vez llegue el extremo del plano y continúe su marcha, añadirá al movimiento precedente, uniforme e inagotable, esta tendencia hacia abajo, debida a la gravedad. Nace así un movimiento descendente naturalmente acelerado... [y enuncia la siguiente proposición] : Un proyectil que se desplaza con un movimiento compuesto por un movimiento horizontal y uniforme y por un movimiento descendente naturalmente acelerado, describe, en este movimiento, una línea semi-parabólica”
De este modo, aplicando el principio de inercia y la modificación de su movimiento por la gravedad, Galileo descubrió que en el Universo eran posibles otras trayectorias diferentes de las rectilíneas y circulares: Las trayectorias parabólicas. Las curvas cónicas fueron estudiadas por Apolonio de Perga (262-190 a. C.) y con una de ellas, la parábola, se podía calcular el alcance y la altura de las trayectorias de los proyectiles que necesitaban los artilleros.
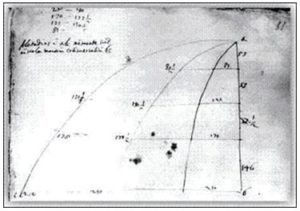
Galileo siguió su razonamiento considerando que, tal y como se observa en el dibujo adjunto, un lanzamiento oblicuo que se inicie en el suelo describía una trayectoria que resulta simétrica respecto de un eje vertical. Ya que se puede considerar la segunda mitad del movimiento como un tiro horizontal que se iniciaría en la posición de mayor altura del tiro oblicuo. Por lo tanto, la trayectoria de un tiro oblicuo se debería obtener componiendo las trayectorias de dos movimientos independientes y perpendiculares entre sí: uno horizontal uniforme y otro vertical uniformemente acelerado, con aceleración igual a g.