
Los números primos son números que solamente son divisibles por ellos mismos y por la unidad. Esta característica junto con la propiedad de que cualquier número entero n mayor que la unidad puede expresarse de manera única, salvo el orden, como un producto de factores primos ha convertido a los números primos en una noción importante en la Teoría de Números. Algunos historiadores remontan el conocimiento de los números primos al Paleolítico Superior y creen que el Hueso de Ishango, de unos 20.000 de antigüedad encontrado cerca de las fuentes del Nilo, en la frontera entre Uganda y la R.D. del Congo es testigo de que los humanos ya pensaban sobre los números primos, ya que aparecen tallados cuatro números primos consecutivos 11, 13, 17, 19. Evidentemente, podría ser sólo una coincidencia, ya que estos números aparecen al hacer una partición de 60 en números impares.
Parece seguro que la primera referencia escrita a los números primos se encuentra en los Elementos de Euclides donde el matemático griego demuestra que los números primos son infinitos. El teorema aparece como la Proposición 20 en el noveno libro de los Elementos enunciado de la siguiente forma: Los números primos son más que cualquier multitud específica de números primos.
A los largo de la historia los matemáticos han intentado obtener una fórmula con la que obtener todos los número primos o al menos una parte de ellos, el problema parece no tener solución, pero la comunidad matemática no desiste de su búsqueda.
Son bastante conocidas algunas fórmulas sencillas, a la vez que curiosas, con las que se pueden obtener algunas colecciones de números primos. Un ejemplo muy popular es el polinomio de L. Euler (1707-1783): n² + n + 41, que da como resultado un total de 40 números primos diferentes al sustituir el valor de n por 0, 1, 2,…,39. Que dan, respectivamente:
41, 43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461 , 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601
Si n = 40 no da un número primo, porque
40² + 40 + 41 = 40(40+1) + 41 = 40·41+ 41= 41(40+1) = 412
Un poco mejor es el polinomio 36n² – 810 n + 2753, con el que se obtienen 45 números primos diferentes para valores de n desde n = 0 hasta n = 44.
Igualmente, el polinomio x2 – x + 41 produce números primos para los valores enteros de x entre 1 y 40.
Otros polinomios que producía números primos fueron los descubiertos por A. M. Legendre (1752-1833), que encontró dos polinomios que generaban números primos: 2x2 + 29, producía números primos para valores enteros de 0 a 28 y el polinomio x2 + x + 17 que ocasionaba números primos para los valores enteros de x entre 0 y 15.
Las investigaciones en este sentido terminaron cuando el matemático Ch. Goldbach (1690-1764) demostró en 1752 que ningún polinomio Q(x) con coeficientes enteros podía generar números primos para todos los valores de x y posteriormente A.M. Legendre probó que ninguna función algebraica racional podía generar siempre números primos. La demostración del resultado de Goldbach fue aproximadamente así:
Teorema: Ningún polinomio puede dar exclusivamente números primos
Demostración:
Sea Q(x) = ao +a1x + a2x2+ a3x3+ … y supongamos que para todo m: Q(m) = p, siendo p primo. Entonces tomemos el valor x = m+np
Q(m+np) = ao +a1(m+np) + a2(m+np)2+ a3(m+np)3+ … ,
desarrollando:
Q(m+np) = ao +a1m + a2m2+ a3m3+ …+ (Múltiplo de p) = p + (Múltiplo de p)
Luego la expresión es divisible por p y por lo tanto Q(m+np) no es un número primo y, por lo tanto, Q(x) no da para x = m+np un número primo
Algunos matemáticos avispados, como el padre M. Mersenne (1588-1648) habían reparado en que entre los números primos, nos encontramos con 3, 7, 31, 127, etc. Todos estos números son de la forma: 22–1, 23–1, 25–1, 27–1. Esta propiedad no sigue cumpliéndose, ya que, en general, no podemos afirmar que 2p – 1 sea primo cuando p es un número primo, ya que. 211 – 1 = 2047 = 23·89, aunque los números 2 13 – 1 = 8191 y 217 – 1 = 131071 sean primos.
No obstante a los números 2n – 1, siendo n un número entero positivo se les llamó números de Mersenne y se planteó la cuestión de buscar números primos entre ese tipo de números.
Los números primos de Mersenne serán de la formar fórmula M(p) = 2p–1, donde p es un número primo. Ya que si n fuera un número compuesto, es decir, n = s·t, entonces:
Haciendo: 2s = x, se tiene que 2n = 2st = (2s)t = xt
El cociente:
![]()
De donde se deduce que: 2n–1 = (2s–1)·(2 s(t –1)+ 2 s(t –2) + … +1)
por lo que 2n–1 es un número compuesto si n es un número compuesto.
Mersenne conjeturó M(p) era número primo para los valores siguientes 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257 y compuesto para los restantes, pero conjetura no se confirmó y se fueron añadiendo nuevos números primos a la lista como M(64), M(61) o M(89). Un prueba de interés que suscitan los números primos es que al principio del siglo XX, sin la ayuda de los ordenadores, ce descubrió que M(257) = 2257– 1 era un número compuesto. Recientemente se descubrió que M(57.885.161) era un número primo de 17 millones de cifras.
Otro tipo de números propuso el matemático francés P. Fermat (1607-1665), el cual formuló la conjetura de que los números de la forma:
![]()
eran primos. En un tiempo en el que no había ordenadores era tarea poco menos que imposible demostrar la primalidad de números tan grandes, pero, en 1732, L. Euler (1707-1783) comprobó que para el quinto número de Fermat, que se obtenía para n = 5, = 4.294.967.297 se podía factorizar y que era igual al producto: 641· 6700417. Con lo que la conjetura de Fermat quedó refutada.
Un teorema importante para números primos es el conocido como Teorema de los Números Primos, enunciado por primera vez por K. F. Gauss (1777-1855) y A. M. Legendre a finales del siglo XVIII, que permite estimar cuántos números primos hay menores que cierto número real x. Y dice que:
Si la función 𝜋(x) nos da el número de números primos menores que x. a medida que x aumenta, el número de primos menores que x , 𝜋(x) , es aproximadamente, x/ln(x), es decir, que:
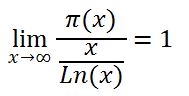
Como 𝜋(x)/x es la probabilidad de elegir un número primo entre los x primeros números naturales, esa probabilidad será, aproximadamente, 1/Ln(x)
