La Aritmética dio paso al Álgebra Literal de las ecuaciones y el Álgebra, que según palabras de J. D’Alembrert (1717-1783) que, siempre da más de lo que se le pide le devuelve agradecida nuevos métodos de contar a la aritmética como es el de método de contar mediante el uso de polinomios y que aquí, con una extralimitación en el lenguaje, le llamaremos método de funciones generatrices. Las funciones generatrices de diferentes tipos fueron inventadas por L. Euler (1707-1783).
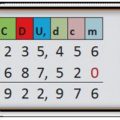
Los cálculos se pueden hacer con cualquier manipulador algegraico, eb este trabajo se ha realizado con DERIVE
PROBLEMA 1. ¿De cuántas maneras se pueden repartir 10 caramelos entre cuatro niños de forma que todos reciban al menos dos caramelos?
Solución 1: Cada niño puede recibir 2, 3 o 4 caramelos. Ninguno puede recibir un número de caramelos mayor o igual que 5, ya que, como se comprueba sin dificultad, en este caso, la exigencia de que el resto reciba al menos dos caramelos no se puede cumplir.
Los niños pueden recibir: 2, 2, 2, 4 o 2, 2,3, 3 caramelos
Por lo tanto:
Recibiendo 2, 2, 2, 4 se puede hacer el reparto de cuatro formas
Recibiendo 2, 2, 3, 3 se puede hacer el reparto de formas diferentes.
En total: de 6 +4 = 10 formas diferentes.
Solución 2: Funciones generatrices
Como cada niño puede recibir 2, 3 o 4 caramelos, la función de cada niño es x2 + x3 + x4. Como hay cuatro niños, la función generatriz será: (x2 + x3 + x4 )4
El número de repartos posibles será el coeficiente de x10 de la función generatriz. Como
(x2 + x3 + x4 )4 = x8 (1 + x + x2 )4
Será el coeficiente de x2 en:
(1 + x + x2 )4 = x 8 + 4·x7 + 10·x6 + 16·x5 + 19·x4 + 16·x3 + 10·x2 + 4·x + 1, que es 10.
PROBLEMA 2. ¿De cuántas maneras se pueden repartir 10 caramelos entre cuatro niños de forma que todos reciban al menos un caramelo?
Solución 1: Cada niño puede recibir 1,2,3,4,5,6 o 7. Ninguno puede recibir más de siete, ya que, como se comprueba sin dificultad, la exigencia de que el resto reciba al menos un caramelo no se puede cumplir en este caso. Los repartos posibles,para repartir 10 caramelos serán:
1117, 1126, 1135, 1144, 1225, 1234, 1333, 2233, 2224
El reparto 1117 se puede hacer de 4 formas
El reparto 1126 se puede hacer de 12 formas
…..
El reparto 1234 se puede hacer de 24 formas
…..
El reparto 2224 se puede hacer de 4 formas
En resumen, el número total de posibles repartos será:
4 + 12+ 12 + 6 + 12 + 24 + 4 + 6 + 4 = 84
Solución 2: Funciones generatrices: Como cada niño puede recibir 1,2,3,4,5,6 o 7 caramelos, la función de cada niño es x + x2 + x3 + x4 + x5 + x6+ x7. Como hay cuatro niños, la función generatriz será:
(x + x2 + x3 + x4 + x5 + x6+ x7)4
El número de repartos posibles será el coeficiente de x10 de la función generatriz.
(x + x2 + x3 + x4 + x5 + x6+ x7)4 = X28 + 4·x27 + 10·x26 + 20·x25 + 35·x24 + 56·x23+ 84·x22+ 116·x21 + 149·x20 + 180·x19 + 206·x18+ 224·x17+ 231·x16 + 224·x15 + 206·x14 + 180·x13 + 149·x12 + 116·x11 + 84·x 10 + 56·x9 + 35·x8 + 20·x7 + 10·x6 + 4·x5 + x4
Es decir 84.
PROBLEMA 3. ¿De cuántas maneras se pueden repartir 10 caramelos entre cuatro niños de forma uno reciba al menos dos y otro al menos tres caramelos?
Solución:
Niños 1 y 2, Pueden no recibir ningún caramelo y como máximo 5, ya que el niño 3 recibe al menos dos caramelos y el niño 4 al menos tres. La función de cada uno de estos niños será:
(1+ x+ x2 + x3 + x4 + x5)
Niño 2.- que recibe al menos dos caramelos: puede recibir 2, 3, 4 , 5, 6 y 7, no puede recibir más, porque el niño 4 recibe al menos tres caramelos. La función de este niño será:
(x2 + x3 + x4 + x5 + x6+ x7 )
Niño 3.- que recibe al menos tres caramelos: puede recibir 3, 4, 5, 6, 7 y 8, no puede recibir más. Porque el niño 4 recibe al menos tres caramelos. La función de este niño será:
(x3 + x4 + x5 + x6+ x7 + x8)
La función generatriz será:
(1+ x+ x2 + x3 + x4 + x5 )2 ( x2 + x3 + x4 + x5 + x6+ x7 ) (x3 + x4 + x5 + x6+ x7 + x8 )
El número de repartos posibles será el coeficiente de x10 de la función generatriz.
(1+ x+ x2 + x3 + x4 + x5 )2 ( x2 + x3 + x4 + x5 + x6+ x7 ) (x3 + x4 + x5 + x6+ x7 + x8 ) =
= x25 + 4·x24 + 10·x13 + 20·x22 + 35·x21 + 56·x20 + 80·x19 + 104·x18 + 125·x17 + 140·x16 + 146·x15 + 140·x14 + 125·x13 + 104·x12 + 80·x11 + 56·x10 + 35·x9+ 20·x8 + 10·x7 + 4·x6 + x5
De 56 formas diferentes
Problema 4. ¿De cuántas maneras se pueden repartir 18 caramelos entre 7 niños de forma Uno reciba al menos un caramelo, dos al menos dos y tres al menos tres caramelos
Solución: Con un camino análogo al anterior será: 210 formas distintas
(x + x2 + x3 + x4 + x5) (x2 + x3+ x4 + x5+ x6)2( x3 + x4 + x5 + x6 + x7)3(1 + x + x2 + x3+ x4) =
= x42+ 7·x41+ 28·x40+ 84·x39+ 210·x38+ 455·x37+ 875·x36+ 1520·x35+ 2415·x34+ 3535·x33+ 4795·x32+ 6055·x31+ 7140·x30 + 7875·x29+ 8135·x28+ 7875·x27+ 7140·x26+ 6055·x25 + 4795·x24 + 3535·x23 + 2415·x22+ 1520·x21+ 875·x20+ 455·x19+ 210·x18+ 84·x17+ 28·x16+ 7·x15 + x14