Aristóteles había observado la caída libre de los cuerpos y concluyó que la velocidad de caída de los cuerpos era directamente proporcional a su peso, es decir, que al dejar caer desde una misma altura cuerpos de pesos distintos sus tiempos de caída serían diferentes y los cuerpos más pesados llegarían al suelo antes que los más ligeros. Esta creencia errónea, ya que una bola de hierro una bola de hierro de un kilogramo caería cien vecese más rápido que otra bola de diez gramos. Pero el error se mantuvo casi dos milenios, sin que nadie refutara su veracidad con mediciones cuidadas.
La razón de que no se hubiera realizado ningún experimento se debía a que la caída libre de los cuerpos se realizaba a tal velocidad que resultaba prácticamente imposible medir el tiempo de caída de un cuerpo y su velocidad porque no había relojes tan precisos. Galileo fue el primero que estudió matemáticamente el movimiento realizando medidas y midiendo los tiempos de caída. Pero esa no fue la única dificultad. Primero Galileo tuvo un punto de inspiración cuando, estudiando el movimiento pendular, reparó en que la velocidad que alcanzaba la bola del péndulo.
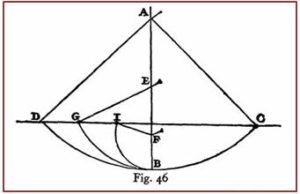
La idea le vino de la observación de que un péndulo de longitud AB que pendía de A y que en el extremo tenía una bola de plomo B. cuando se le interponía un clavo E en una posición intermedia en la vertical AB, modificando con ello la longitud del péndulo, en el punto más bajo de la trayectoria la velocidad era la misma en ambos sentidos de la oscilación, ya que en los dos alcanzaba la misma altura. Por lo tanto, la velocidad de la bola en el punto más bajo no dependía de la longitud del péndulo, sino de la altura de la que partía la oscilación.
Con esa observación, Galileo vislumbró la similitud entre el péndulo y el plano inclinado y pensó que si una bola rodaba por un plano inclinado y a continuación se encontraba otro plano inclinado hacia arriba y seguía su movimiento, la bola alcanzaría la misma altura que la del punto del que partió, tal y como sucedía con el péndulo. Y, como ocurría en el péndulo, la altura alcanzada no dependía de la pendiente del segundo plano sino la velocidad con que iniciara la subida. Por lo tanto, (y esta es la observación genial de Galileo) la velocidad con que una bola, que descienda por un plano inclinado desde el reposo hasta el suelo no dependerá de la inclinación del plano con respecto a la horizontal, sino de la altura o desnivel vertical del que hubiera partido.
Galileo midió la velocidad de caída de un cuerpo con las siguientes ideas básicas:
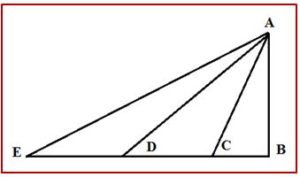
Primera: Reparó en que las velocidades alcanzadas por un mismo móvil, en planos de diferente inclinación, son iguales cuando las alturas de los mismos planos son también iguales. Es decir que si dejamos caer libremente unas bolas verticalmente o deslizándose por los planos AC, AD, o AF, las velocidades que alcanzan en los puntos B, C, D, E son las mismas.
Segunda: Con la observación anterior la tarea de medir la velocidad de caída libre de un cuerpo se podía hacer calculando la velocidad de caída por un plano inclinado que tardaba más tiempo en alcanzar la velocidad. Galileo había conseguido aumentar el tiempo que tardaba un cuerpo alcanzar una velocidad, puesto que tardaba más deslizarse por el plano inclinado AE que la caída libre AB. Para medir el tiempo recurrió a la clepsidra o reloj de agua, que consiste en una vasija grande llena de agua, que podía verter un hilillo de agua, que recogía en una probeta durante todo el tiempo que la bola descendía. Luego pesaba el agua recogida en cada descenso con lo que relaciones entre los pesos de agua daban relaciones entre de los tiempos de descenso.
Tercera: Con el reloj de agua midió el tiempo empleado para recorrer diferentes partes de un plano inclinado un ángulo α con la horizontal al que le había practicado con un canalillo y encerado para evitar desviaciones y, en lo posible, el rozamiento.
Midiendo las distancias recorridas por una bola que se deslizaba libremente desde la parte más alta sobre un plano inclinado, observó que en el primer intervalo de tiempo recorría una distancia L, en el segundo intervalo 3L, en tercero 5L, en el cuarto 7L, en el enésimo (2n-1) L. De donde obtuvo las siguientes conclusiones: (supondremos L lo expresamos en centímetros y que cada intervalo de tiempo es un segundo)
Conclusión 1.– El movimiento era uniformemente acelerado ya que el espacio recorrido cada segundo (la velocidad) aumentaba 2L cm/s, luego la aceleración era de 2L cm/s2.
Conclusión 2.- El espacio s recorrido en t segundos era proporcional a t2, ya que
s = L + 3L + 5L + 7L + ···+ (2t-1) L =
= [1 + 3 + 5 + 7 + ··· + (2t-1)] L = t2·L = t2·L,
Como la aceleración a = 2L, se obtiene:
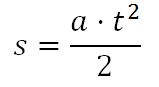
Por tanto, la distancia total recorrida durante cierto período de tiempo era proporcional al cuadrado de este tiempo
Conclusión 3.- Las distancias recorridas en intervalos sucesivos de tiempo estaban en la proporción 1 : 3 : 5 : 7, etc. siempre, Cuanto más inclinado estaba el plano mayores era las distancias recorridas, pero sus relaciones seguían siendo las mismas. Galileo, concluyó que esas relaciones se debían cumplir cuando el ángulo α = 90º, esto es para la caída vertical
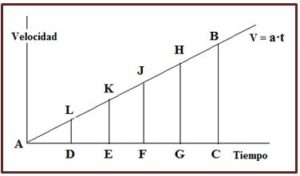
Conclusión 4.- Galileo dedujo que la velocidad el movimiento uniformemente acelerado era proporcional tiempo: vt = a·t. Como la velocidad aumenta cada segundo una cantidad fija a Si conocemos la velocidad en el instante inicial v0 y al cabo de t segundos vt se tiene que vt – v0 = a·t y como v0 = 0, entonces vt = a·t.
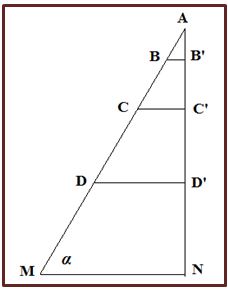
Conclusión 5.- Para calcular g, que es la aceleración cuando el plano está vertical realizó un razonamiento que expreso en lenguaje actualizado como sigue:
Si una bola desciende por un plano inclinado AM, adquirirá una aceleración a y recorre el plano en un tiempo t, el espacio recorrido y la velocidad de la bola cuando llega al suelo serán respectivamente:
Si la bola desciende en caída libre por la vertical AN, adquirirá una aceleración g y tardará un tiempo t’, pero en los puntos B y B’, C y C’ y en todos los que definen una línea paralela a la horizontal llevarán la misma velocidad:
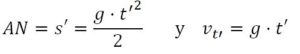
Dividiendo ambas ecuaciones y teniendo en cuenta que AN = s’ = s·sen α, siendo el ángulo que forma el plano con la horizontal
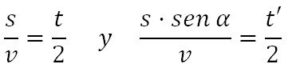
De dónde se obtiene que t’ = t· sen α
Y como la velocidad con que llegan suelo ambas bolas es la misma;
vt = vt’ ⇒ a·t = g·t’
entonces a·t = t·g·sen α y, por lo tanto: a = g·sen α
Galileo, para calcular la aceleración gravitatoria, g, midió la aceleración, a, en un plano con un ángulo de inclinación α respecto a la horizontal y obtuvo:
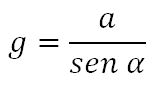
«Totalmente de acuerdo, muy acertado el artculo, enhorabuena»