Crecer es darse cuenta de que la vida no es lo que esperas. Es comprobar que unas veces se gana y otras se pierde. Y, sobre todo, que, a veces, se gana y se pierde al mismo tiempo. Patrick Ness (Un monstruo viene a verme)
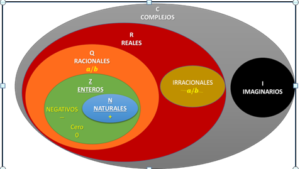
En la actualidad cualquier estudiante de Enseñanza Media conoce las razones por las fue necesario ampliar el conjunto de de los números desde los números naturales hasta los números complejos. Los naturales se amplían a los números enteros, los enteros los números racionales, los racionales en los reales y éstos a los números complejos.. Los estudiantes realizan con soltura operaciones con números enteros, con números racionales, los números reales y e incluso los números complejos.
Las sucesivas ampliaciones de los números naturales se hicieron por ganar en operatividad y poder realizar las diferentes operaciones aritméticas. Pero con cada ampliación numérica también se perdían algunas propiedades importantes que contribuyeron a que la noción de número se fuera haciendo cada vez más compleja y llena de matices.
Al llegar a la cumbre de los números complejos desde los números naturales se habían perdido ciertas propiedades intuitivas que hicieron decir a Kronecker su famosa frase: Dios creó a los números enteros y el hombre hizo todo lo demás. Con lo que queriá decir que Dios había introducido en la mente del hombre los números naturales, es decir que la noción de número natural es una idea innata y que los demás números son invención humana, construidos por el hombre por las necesidades del cálculo y que ya no eran número tan intuitivos, ni tan naturales.
A continuación haremos un resumen de lo que se ganó y de lo que se perdió con cada ampliación numérica tratando de efectuar un balance del proceso:
1.- Ganancias y pérdidas con la ampliación de los números naturales a los enteros:
En el conjunto N = {0, 1, 2, 3, …} de los números naturales se pueden las operaciones suma y producto de cualquier pareja de números, pero no se podía realizar la operación inversa de la suma. Dentro del N, no era posible realizar operaciones como 4 – 7, (aquellas en las que el minuendo es menor que es sustrayendo), ya que el resultado sería una deuda de -3 y este número no pertenece a N. Para poder realizar la resta el conjunto N se amplía al conjunto Z = {… -3, -2, -1, 0, 1, 2, 3, …} y en este conjunto la resta es una operación interna.
En esta ampliación numérica de N a Z ganamos en operatividad, ya que se pueda hacer la diferencia de cualquier pareja de números, pero también se pierde algo y es que, perdemos que el conjunto Z posea primer elemento, un elemento mínimo.
2.- Ganancias y pérdidas con la ampliación de con la ampliación de los números enteros a los números racionales
Con esta ampliación se consiguió que se pudiera realizar el cociente de cualquier pareja de números enteros. En el conjunto Z no era posible realizar la operación 4/5, ya que el resultado sería 0,8 que no es un número entero, es un número racional y la operación se puede realizar en Q, ya que es el conjunto

Por lo tanto, dentro de Q , podemos realizar la suma la resta y producto y el cociente de cualquier par de números enteros.
En la ampliación de Z a Q ganamos que se puedan hacer dentro de él las operaciones suma, resta, producto o cociente de cualquier pareja de números. Pero también se pierde algo y es la contigüidad, es decir, cuál saber, por ejemplo, quien es el número siguiente de 0,77 en el conjunto Q. En el conjunto de los números enteros los elementos contiguos del número a son a-1 y a+1. Pero ¿cuál es el número racional siguiente de 0,77 podemos emprender un proceso indefinido: 0,771, 0,7701, 0,77001, 0,770001, 0,7700001…. sin que nunca lo podamos alcanzar.
3.- Ganancias y pérdidas con la ampliación ampliación de los números racionales a los números reales
También es esta ampliación se ganaron y perdieron cosas. La ampliación de los números racionales a los números reales a se pueden entender como completar la recta. Los griegos demostraron que había número que no se podían expresar en forma de fracción. Entre dos número racionales hay números que no son racionales. El conjunto R de los números reales es el conjunto continuo, que representado sobre la recta le corresponde un número. Es el conjunto de los números racionales y los irracionales.
En el paso de Q a R, se completaba la recta hasta tener el continuo, es decir que a cada punto de la recta le correspondía un número real. Pero, sin embargo, en la ampliación de Q a R se perdió algo tan importante como la numerabilidad.. Los números reales no se podían contar con los números naturales. Con los números reales no es posible hacer una lista que los contenga a todos. Los números racionales eran numerables, pero los números reales son un conjunto infinito de orden superior, es un infinito de la potencia del continuo.
4.- Ganancias y pérdidas con la ampliación ampliación la ampliación de los números reales a los números complejos
En este conjunto de los números complejos se pueden calcular raíces cuadradas de número negativos. El conjunto de los números complejos se forma un nuevo conjunto numérico que tiene dos tipos de unidades diferentes: unidades reales y unidades imaginarias, de la forma a + bi. Donde i es laraizcuadrada de -1
C = {(a + bi) | a, b ∊ R}
En este conjunto numérico se pueden hacer todas las operaciones. No obstante, al ampliar R a C se pierde una propiedad importantísima y es el orden. Los números complejos no pueden tener un orden compatible los números reales.
Para probarlo supongamos que pudiéramos definir un orden para todos los números complejos a + bi compatible con el orden de los números reales. Una de las propiedades es que dos números distintos cualesquiera a y b tienen que ser comparables (a > b o b > a). Veamos que ocurre cuando comparamos la unidad imaginaria i con el cero:
a) Si suponemos que i < 0 y multiplicamos ambos miembros de la desigualdad por i (como suponemos que i es negativo):
Si i < 0 ⇒ i2 > 0 ⇒ -1 > 0 lo cual es falso.
b) Pero, si suponemos que i > 0 y multiplicamos ambos miembros de la desigualdad por i (que ahora suponemos positivo):
Si i > 0 ⇒ i2 > 0 ⇒ -1 > 0 lo cual es falso.
Por lo tanto i no es mayor que cero ni cero es mayor que i, lo que significa que i y cero no son comparables. Por tanto, como acabamos de ver, no podemos definir una relación de orden en el conjunto de los números complejos cuya restricción a los números reales sea la relación de orden con las propiedades habituales de orden de los números reales. Los números complejos, por lo tanto, no están ordenados como los número reales.