Jacob Bernoulli (1645-1705) era miembro de una familia de comerciantes de Ámsterdam, que abandonó la ciudad durante la Guerra de Flandes (1568-1648) y se estableció en la ciudad suiza de Basilea. Su abuelo, en 1622, ya era ciudadano de Basilea y su padre, Nicolás, siguió con el negocio familiar y llegó a ser consejero del municipio y magistrado de la ciudad.
Jacob fue el primero de esta familia de comerciantes que se dedicó al estudio de las matemáticas. Abriendo la saga familiar más famosa, brillante e influyente del siglo XVIII, (siete matemáticos de primera línea) y de la historia de las matemáticas.
Siguiendo los deseos de su padre estudió teología en la universidad de Basilea donde se graduó en 1676, pero su pasión por las matemáticas lo llevó a estudiar los dos años siguientes en París con N. Malebranche (1638-1715) y con otros cartesianos. En 1681 estudió con el matemático holandés J. Hudde (1628-1604) , en Inglaterra, donde conoció a R. Boyle (1627-1691) y también a R. Hooke (1635-1703). A su regreso a Basilea en 1683, comenzó a dar clases de ciencias experimentales y a publicar sus artículos en la revista alemana Acta Eruditorum, recientemente creada pos iniciativa de G. Leibniz (1646-1715). Realizó grandes avances en el Cálculo Infinitesimal y muchas aplicaciones del mismo al estudio del movimiento, estudió la curva isócrona. En 1687, año de la publicación de los Principia de Newton, obtuvo la cátedra de matemáticas en la Universidad de Basilea, cargo que mantuvo hasta su muerte.
Jacob Bernoulli realizó valiosas aportaciones la Teoría de la Probabilidad, su trabajo más destacado en este campo está recogido obra póstuma Ars Conjectandi (1713). Es el libro se consolidaron muchos temas de cálculo combinatorio y algunas ideas centrales en la teoría de la probabilidad, como la ley de los grandes números. El libro se considera como trabajo fundacional tanto en teoría de la probabilidad como en la combinatoria. El trabajo un gran impacto tanto tan importantes como, A. de Moivre (1667-1754) .
De este trabajo vamos adaptar un problema de Teoría de Probabilidades en el que interviene el concepto de combinaciones con repetición resuelto por Jacob Bernoulli con un ingenioso recurso de cálculo combinatoria
En primer lugar recordaremos dos conceptos;
Permutaciones ordinarias (de elementos diferentes): Permutaciones ordinarias de n elementos son las distintas reordenaciones que se pueden hacer con n elementos distintos. El número de permutaciones se representa por Pn.
Pn = n·(n-1)·(n-2) ··· 3·2·1
Permutaciones con repetición (cuando hay elementos repetidos) Permutaciones con repetición de n elementos son las distintas reordenaciones de los n elementos cuando hay elementos que se repiten, por ejemplo, uno se repite a veces, otro b … hasta el enésimo que se repite k veces, donde, por tanto, a + b + c + …+ k = n. Consideramos dos ordenaciones distintas si difieren en el orden de colocación de algún elemento (distinguible).
Denotaremos a este tipo de permutación como:
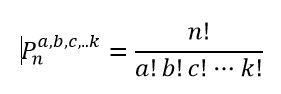
Combinaciones con repetición de m elementos tomados de n en n son los distintos grupos de n elementos iguales o distintos que se pueden formar con los m elementos, de forma que dos grupos son diferentes cuando se diferencian en algún elemento y no en el orden de colocación.
Problema: ¿De cuántas maneras diferentes se pueden comprar 7 refrescos, en una tienda donde lo ofrecen en 4 sabores diferentes (Limón, naranja, piña y pera) sin mezclarlos?
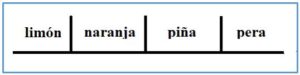
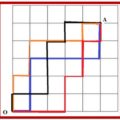
Evidentemente, podremos comprar todos de un sabor, de dos sabores, de tres, etc. con la única condición de tomar exactamente siete refrescos. En el gráfico adjunto se representa esquemáticamente la posible distribución de los refrescos, para los que bastan tres tabiques para separar los sabores de los refrescos.
Si designamos los refrescos con ceros (habrá 7 ceros) y los tabiques con unos (habrá tres unos), podemos establecer lo siguiente:
0010001001, significa dos de limón, tres de naranja y dos de piña (ninguno de pera)
0100001010, significa uno de limón, cuatro de naranja, uno de piña y uno de pera
1000001001, significa cero de limón, cinco de naranja y dos de piña y cero de pera
De este modo, establecemos una correspondencia biyectiva entre las posibilidades de la compra de refrescos y los números (en binario) que se pueden formar con siete ceros (número de refrescos que deseamos comprar) y tres unos (número de sabores de refrescos que podemos elegir menos uno). Es decir, con diez elementos en los que se repiten siete (los refrescos) y los tres tabiques de separación, que, dependiendo de su ubicación, determinan el número de refrescos seleccionados de cada clase entre los siete elegidos. Lo que podemos escribir en las formas:
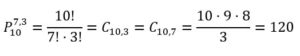
Por lo tanto, podemos elegir los siete refrescos de 120 maneras.