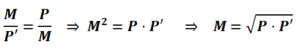Una balanza consta de dos platos que cuelgan de los extremos de una barra horizontal con un punto de apoyo en el centro de la misma. Si la balanza está en equilibrio, la balanza está nivelada y la barra permanece horizontal cuando está en equilibrio. Los dos brazos de la balanza deben ser iguales y ser de un material homogéneo, para que su diferente longitud o su distinta densidad influyan en la pesada. A continuación analizamos una cuestión de un tendero tramposo que tenía una balanza cuya barra era de un material homogéneo, pero de brazos desiguales.
Un vendedor algo desaprensivo tenía una balanza defectuosa que tenía brazos desiguales, de longitudes 50 y 45 centímetros respectivamente y se le ocurrió que la podía utilizar para comprar y vender con ventaja haciendo trampas con el peso y engañando a proveedores y a clientes.
Su estrategia era muy clara, cuando compraba colocaba la mercancía en el platillo que colgaba del brazo corto con lo que, por la ley de la palanca, debía colocar menos pesas de las debidas en el otro platillo, y ganaba porque era por esas pesas por lo que pagaba. Mientras que para vender colocaba la mercancía en el platillo del brazo largo y obtenía otra ganancia adicional. ¿Cuál es el beneficio fraudulento de este avispado, tramposo poco íntegro comerciante?
Supongamos que compra M kg reales de cierta mercancía que equilibra con un peso P. Para timar a los compradores coloca la mercancía en el platillo que pende del brazo corto y en otro platillo equilibra con pesas
Ganancia primera: Compra M kg y paga por P kg
M · 45 = P · 50.
De donde P = 0,9 M, y el tendero ha timado al proveedor 0,1· M kg de mercancía, y no satisfecho con eso, a la hora de vender, cambia de platillo, es decir, pone la mercancía en el platillo de brazo largo y equilibra con un peso P’ con pesas en el platillo del otro brazo
P’· 45 = M · 50
Ahora ha timado a su comprador: 0,11· M. En total ha timado el 21 %.
Finalmente terminamos con una pregunta: ¿Hubiera podido nuestro tendero con su balanza defectuosa y con pesas suficientes haber conocido exactamente el peso M de la mercancía?
La respuesta es que si, el peso de la mercancía es la raíz cuadrada del producto de los pesos fraudulentos, como se observa acontinuación:
M · 45 = P · 50.
P’· 45 = M · 50
De donde, dividiendo miembro a miembro, se obtiene: