
Nicómaco de Gerasa (Siglo I) perteneció a la escuela neopitagórica y fue el primer matemático que separó por completo la Aritmética de la Geometría, que era la matemática dominante en Grecia. Su obra original no se ha conservado, no obstante, su Introducción a la Aritmética es conocida gracias a la traducción latina de Boecio (480- 524) y fue libro de texto en las Universidades durante toda la Edad Media.
La Aritmética de Nicómaco, como señala Morris Kline, tiene una enorme importancia porque los números, al separarse de la geometría, dejaron de ser considerados como longitudes de líneas, aunque aparecen como entes cargados de cierto misticismo. En su Aritmética aparecen números cuadrados, cubos, triangulares, oblongos, primos, compuestos, amigos, perfectos, abundantes deficientes y otros muchos y, además, se recoge la tradición mágica de la Numerología Pitagórica y la Teoría Mística del Universo con los números.
En esta Aritmética se estudiaban relaciones numéricas curiosas que no se podían vislumbrar desde la Geometría Euclidiana. Un ejemplo de un resultado interesante es el siguiente: Cualquier cubo se puede expresar como diferencia de dos cuadrados. Esta propiedad rompía las reglas de homogeneidad geométrica, parecía indicar que un volumen se podía expresar como diferencia de dos áreas.
Esta afirmación anterior es fácilmente observable como puede comprobarse a continuación:
23 = 32 – 12 33 = 62 – 32 43 =102– 62 53 = 152– 102 63 =212– 152
Podemos preguntarnos si esta relación la cumple cualquier número natural elevado al cubo
Para realizar esta demostración nos apoyaremos en dos resultados.
Primer resultado: La suma de los n primeros números naturales es
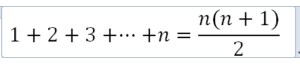
Podemos interpretar la fórmula obtenida como la mitad del área de un rectángulo de dimensiones n·(n+1).
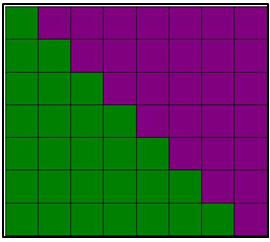
Los griegos tenían una demostración geométrica que puede observarse en la figura adjunta en la que en un rectángulo de dimensiones 7×8 se ha descompuesto en dos triángulos escalonados de área 1 + 2 + 3 + 4 + 5 + 6+ 7 luego:
![]()
Segundo resultado: La suma de los n primeros números impares es n2.
1 + 3 + 5 + ··· + (2n-1) = n2
Para ellos haremos una demostración gráfica como muy en la línea de la aritmética griega basada en la geometría y en la representación geométrica de los números, así:
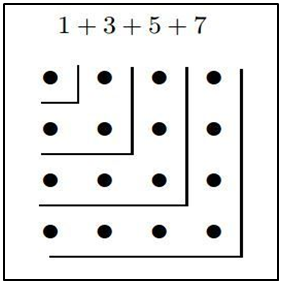
Al representar la suma los impares sucesivos se pueden ordenar formando cuadrados. Cada cuadrado sucesivo tiene un lado una unidad mayor, como puede observarse en la figura. La figura seguiría siendo un cuadrado añadiéndole 9 elementos más, luego 11 y así sucesivamente (la semejanza de las figuras geométricas suplía para los griegos al principio de inducción).
Para demostrar que cualquier cubo se puede expresar como diferencia de dos cuadrados observemos lo siguiente:
![]()
Es decir, observamos que
- 1, es un cubo,
- La suma de los dos impares siguientes (3 y 5) es 23 =8
- La suma de los tres impares siguientes (7, 9 y 11) es 33 =27
- La suma de los cuatro impares siguientes (13, 15, 17, 19) es 43 = 64
- La suma de los cinco impares siguientes (21+23+25+27+29) es 53 = 125
……..
Además, se observa que, por ejemplo que 43 = 64 tiene delante 1 + 2 + 3 números impares consecutivos y es suma de los cuatro impares consecutivos siguientes.
Igualmente, que 53 = 125 tiene delante 1 + 2 + 3 + 4 números impares consecutivos y es suma de los cinco impares consecutivos siguientes.
Igualmente, n3 tendrá delante 1+2+3+···+(n-1) números impares consecutivos y es suma de los n impares consecutivos siguientes
Debemos comprobar que n3 aparece sumando los números impares comprendidos el lugar 1+2+3+···+(n-1)+1 y el lugar 1+2+3+···+(n-1)+n. Para ello observemos que
La suma de los 1 + 2 + 3 +···+ (n-1) + n primeros números impares es:

La suma de los 1 + 2 + 3 +···+ (n-1) primeros números impares es

Su diferencia:


que es un cubo que es lo que deseábamos comprobar.




