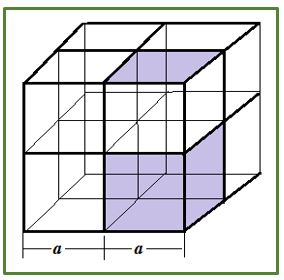
El problema conocido como problema de Delos o de la duplicación del cubo. Los orígenes de este problema se remontan a la leyenda. En la historia de las matemáticas ha habido cuestiones que no han encontrado solución hasta que no se han abordado desde un punto de vista superior, más abstracto. Esto se ha producido en la resolución de diversos problemas como sucedió con los tres problemas clásicos griegos, la demostración de la imposibilidad de hallar una solución por radicales de la ecuación de quinto grado, la solución del ultimo teorema de Fermat y con la forma de abordar muchos otros problemas que cuya solución se ha obtenido atacándolos desde un nivel de abstracción superior.
Uno de estos problemas es conocido como problema de Delos o de la duplicación del cubo. Los orígenes de este problema se remontan a la leyenda. La historia más completa de este problema la relató Eratóstenes en su obra La duplicación del cubo, obra que dedicó al rey Ptolomeo. Eratóstenes contó la historia diciendo que cierto autor trágico, seguramente Eurípides, hizo aparecer en escena a Minos en el momento que construía la tumba de su hijo Glauco, y al observar que solamente medía cien pies por cada lado dijo: es un espacio muy pequeño para sepulcro de un rey. Duplicadla conservando su forma cúbica duplicando cada lado.
Para cumplir con la respuesta del oráculo los atenienses dedicaron a Apolo un altar de lado doble que el anterior, pero la peste siguió ya que no se había se había cumplido a la indicación del oráculo, puesto que no habían duplicado el altar, sino que lo habían hecho ocho veces mayor. El problema también se propuso resolverlo mediante la regla y el compás.
La limitación de la matemática griega de realizar las operaciones con regla y compas se debía a que, en el siglo V, la escuela pitagórica había descubierto la existencia de magnitudes irracionales que no estaban formadas por partes alícuotas de la unidad y no se podían expresar como fracciones de números enteros. No obstante, los griegos aceptaron las magnitudes que se podían construir con regla y compás. Con el compás se trazaban circunferencias y con la regla rectas. La geometría analítica hizo ver que las circunferencias podían expresarse con ecuaciones de segundo grado y las rectas con ecuaciones de primer grado. Por tanto, los problemas con regla y compás podrían reducirse a la resolución de sistemas de ecuaciones de segundo grado.
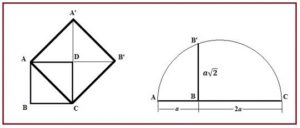
Hipócrates de Quios (470-410 a de J.C.) sabía que para calcular el lado de un cuadrado cuya superficie fuera igual a la de un rectángulo de lados a y b se insertaba una media proporcional entre a y b, de modo que el lado del cuadrado era x verificaba que x =√ab. Hipócrates determinaba x del siguiente modo geométrico que se muestra, que es un método gráfico de determinar la media geométrica. Para determinar un cuadrado de área doble que otro de lado a basta con insertar una media proporcional entre a y 2a, y se obtiene un lado x = a √2, tal y como se indica en la construcción siguiente:
Los geómetras generalizaron el procedimiento empleado para la duplicación del cuadrado a la duplicación del cubo. Hipócrates descubrió que el problema de calcular el lado un cubo de volumen doble a otro cubo dado de lado a era equivalente al de determinar dos medias proporcionales entre 2a y a. Esto es, hallar dos valores x e y que satisfagan la relación:
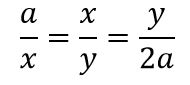
El no encontró la forma de construir con regla y compas dos medias proporcionales entre a y 2a, aunque los científicos griegos diseñaron algunos mecanismos que permitían resolver el problema dejando aparte las potentes restricciones que imponía el uso exclusivo de la regla y el compás. Eratóstenes de Cirene (284-192 a.J.C.) construyó un aparato mecánico, llamado mesolabio que permitía insertar un número cualquiera de medias proporcionales entre dos magnitudes dadas.
Realmente intercalar dos medas proporcionales entre a y 2a era equivalente a resolver el sistema de ecuaciones:
ay = x2 y y2= 2ax,
eliminando el medio y de ambas ecuaciones se obtiene que 2a3 = x3, es decir, que:
![]()
Es decir, la resolución del problema de la duplicación del cubo se reduce a calcular raíces cúbicas y, más precisamente, a resolver la ecuación x3 – 2 = 0, lo que supone cambiar de plantearse un problema de construcciones geométricas a un problema puramente algebraico. Un cambio de punto de vista de la geometría al algebra, que supone una traslación del problema y un mayor grado de abstracción. Dejamos de tener contacto con la imagen del cubo.
En primer lugar probaremos la irracionalidad de la raíz cubica partiendo de la ecuación:
![]()
Supongamos que:

Por lo tanto, a = 2a1 (a y a1 primos entre sí). Luego:
2b3 = 8(a1)3 ⇒ b3 = 4(a1)3
Pero, como a y b hemos supuesto que eran primos entre sí, entonces a1 y b son primos entre sí, por tanto 4| b3 y 2|b, por consiguiente , a y b son divisible por dos y la fracción no es irreducible contrala hipótesis supuesta. Por lo tanto, la raíz cúbica de 2 no es un número racional. Pero ¿es un número que se pueda construir con regla y compás?
Seguiré los pasos Courant, R. y Robbins H. en ¿qué es la matemática?
- Supongamos que la raíz cúbica de 2 se puede obtener a partir de Q con regla y compás (ecuaciones de segundo grado), añadiendo sucesivamente las raíces cuadradas necesarias. La raíz cúbica de 2 no pertenece a Q, porque es un número irracional
Podemos suponer que pertenece a alguna extensión Fk del cuerpo Q de los números racionales que se obtiene añadiendo a Q raíces cuadradas.
Fk = Q [√m0, √m1, ….√mk-1, ]
Sea la sucesión
Q = F0 ⸦ F1 = F0[√m0] ⸦ F2 = F1[√m1] ⸦ … ⸦ Fk = Fk-1[√m k-1]
Donde mk-1∈ Fk-1
- Si Fk es la primera extensión tal que:
![]()
entonces x puede escribirse en la forma x = p + q √ω, donde p y q ∈Fk-1.
Si x = p + q √ω es solución de x3 – 2 = 0 Entonces, como x pertenece a Fk , se tiene que x3 y x3 – 2 pertenecen a Fk, por lo tanto se verifica que x3 – 2 = a + b √ω, donde a y b ∈Fk-1. También será solución y = p – q √ω.
Por ser p + q √ω solución:
(p + q √ω)3 – 2 = p3 + q3ω√ω + 3p2q√ω + 3pq2ω – 2 =
= [p3+ 3pq2ω – 2] + [q3ω + 3p2q]√ω ⇒
x3 – 2 = a + b √ω = 0 ⇒
⇒ a = [p3+ 3pq2ω – 2] y b = [q3ω + 3p2q] = 0
Y, de aquí y = p – q √ω también será solución:
(p – q √ω)3 – 2 = p3 – q3ω√ω – 3p2q√ω + 3pq2ω – 2 =
= [p3+ 3pq2ω – 2] – [q3ω + 3p2q]√ω ⇒
y3 – 2 = a – b √ω = 0
tenemos dos soluciones distintas: x = p + q √ω e y = p – q √ω y que x – y = 2q√ω sólo puede anularse si q = 0, pero si q = 0 ⇒ x = p ∈ Fk-1 contra la hipótesis, que era que Fk es la primera extensión tal que:
![]()
Con lo que la raíz cúbica no puede obtenerse mediante combinaciones de raíces cuadradas. Además, hemos probado que tendría dos soluciones reales diferentes lo que supone una contradicción, ya que la ecuación propuesta tiene una sola solución real. Por tanto, el lado del cubo de doble volumen no se puede constrir geométricamente con recla y compás como planteaba el problema de Delos.
VÍCTOR ARENZANA HERNANDEZ


