En algunos problemas de matemáticas se conocen algunos datos que no son claramente numéricos y llaman la atención. Esto ocurre cuando se plantean cuestiones como la siguiente:
Juan le dice a un amigo que tiene dos hijas menores de diez años cuyo producto de edades es 36 y le pregunta ¿Cuál es la edad de mis hijas?
Por ser menores de diez años sus edades no pueden ser 1 y 36 años, ni tampoco 2 y 18 años, ni 3 y 12. Resulta evidente que las edades de las hijas únicamente pueden ser 4 y 9 años o bien 6 y 6 años. El amigo se da cuenta y le dice que tiene dos posibilidades y que, por lo tanto, no le puede saber a lo que Juan le responde: la mayor toca el piano. Con esa respuesta le quiere decir que una de sus hijas es mayor que la otra, luego no pueden tener 6 y 6 años y sus edades deben ser 9 y 4 años.
El problema siguiente es un clásico que figura en muchas colecciones de problemas curiosos, expuesto en forma parecida a la siguiente:
PROBLEMA 1.- Un matemático se encuentra por la calle con un amigo que le pregunta ¿Cuántos hijos tienes? El matemático le respondió que tenía tres hijas y su amigo le preguntó qué edades tenían a lo que el matemático le respondió: El producto de sus edades es 36 y su suma es el número de la casa que tenemos delante. El amigo, después de hacer unos cálculos, le dijo: “para saber las edades de tus hijas me falta un dato”, a lo que el matemático le respondió, es verdad, la mayor de mis hijas toca el piano. ¿Cuáles son las edades de las hijas del matemático?
Para resolver el problema comenzaremos descomponiendo el número 36 en producto de tres factores, los cuales serán las posibles edades de las tres hijas del matemático. Las posibilidades de un producto de tres números naturales igual a 36 son las siguientes:
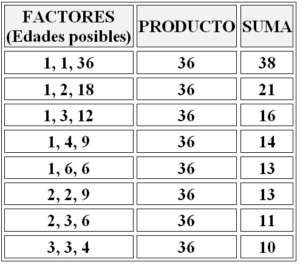
Ahora debemos razonar desde el punto de vista del amigo del matemático que posee un dato que nosotros desconocemos. El amigo conoce el número de la casa, el cual representa la suma de las edades de las tres hijas y podría resolver el problema siempre y cuando el número de la casa no fuera 13, porque en ese caso existirían dos posibilidades (1, 6 y 6 años ó 2, 2 y 9 años).
Por eso tiene que solicitar más pistas y recibe la información: la mayor toca el piano. Este dato le permite decidir entre las dos opciones, porque ahora sabe que una de las hijas es mayor que las otras dos, por lo que no cabe la solución 1, 6 y 6 años, porque hay dos mayores y la solución debe ser 2, 2 y 9 años.
Un problema análogo es el siguiente:
PROBLEMA 2.- La suma de las edades de dos hermanos es un tercio de su producto y el mayor toca el piano ¿Cuántos años tiene cada uno?
Para resolver el problema habrá que buscar las soluciones enteras y positivas de la ecuación:
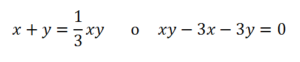que se resuelve fácilmente teniendo en cuenta que :
(x – 3)·(y – 3) – 9 = xy – 3x – 3y
Por lo tanto hallar las soluciones enteras y positivas de xy – 3x – 3y = 0 es equivalente a calcular las soluciones enteras y positivas de (x – 3)·(y – 3) = 9
Para calcular las soluciones razonaremos así: puesto que (x – 3) debe ser un factor entero de 9, puede tomar los valores 1, 3 y 9, entnces:
- Si (x – 3) = 1 ⇒ (y – 3) = 9 ⇒ x = 4 y = 12
- Si (x – 3) = 3 ⇒ (y – 3) = 3 ⇒ x = 6 y = 6
- Si (x – 3) = 9 ⇒ (y – 3) = 1 ⇒ x = 12 y = 4
Luego, como el mayor toca el piano, las edades no pueden ser 6 y 6 años y las edades de los hermanos serán 4 y 12 años.
