Cuenta a leyenda que el Rey Hierón II de Siracusa (306-215 a. C.) había encargado a un orfebre diseñar y confeccionar una corona de oro y que para fabricarla le entregó un lingote de oro puro al artista. Cuando el orfebre terminó la corona el rey quedó satisfecho con el resultado. Comprobó que la corona pesaba exactamente lo mismo que el lingote, pero le llegaron dudas sobre la honradez del artesano y sospechó que le había engañado sustituyendo, a la hora de fundir el lingote, parte del oro por algún material más barato, como la plata.
Al rey Hierón le gustaba la corona y no quería destruirla para averiguar su composición, pero expuso sus sospechas a Arquímedes (287 – 212 a. C.), que era el mejor de la matemáticos griegos de su época y uno de los más grandes científicos de todos los tiempos, y le propuso que determinara si el artista lo había engañado sin romper la corona, ni cortarla, ni fundirla, porque el orfebre podía ser un pillo, pero la corona era bellísima.
Este relato se considera como una leyenda porque se cuenta por primera vez en la obra De architectura de Vitruvio (80 a.C-15d.C), que fue arquitecto de Julio César, y la obra fue escrita aproximadamente dos siglos después de la muerte de Arquímedes.
Cuenta Vitruvio que Arquímedes comenzó a pensar sobre el problema inmediatamente y le dio vueltas y vueltas a la cuestión hasta el punto que no se separaba de la corona en ningún momento del día. Hasta que un día, al meterse en la bañera se le ocurrió como abordar el problema y resolverlo.
Se le ocurrió que el volumen del agua que se desplazaba la corona al sumergirla en el agua tenía que ser igual al volumen de la corona, por lo tanto, si medía el agua que rebosaba al meter la corona en un recipiente completamente lleno de agua, conocería el volumen de la misma y luego podría compararlo con el volumen de un objeto de oro (un lingote) del mismo peso que la corona y si midiendo ambos volúmenes resultaran ser diferentes, sería una prueba concluyente de que la corona no era de oro puro.
Vitruvio dice que esta idea se le ocurrió a Arquímedes mientras se estaba bañando y que, por la excitación que le produjo el descubrimiento, salió del baño desnudo hacia el palacio de Hieron gritando ¡Eureka!, ¡Eureka!, que significa: «¡Lo encontré! ¡Lo encontré!».
Eso es la historia del descubrimiento del Principio de Arquímedes en forma literaria, pero la realidad es que Arquímedes, en su obra Sobre los cuerpos flotantes, en la que sentó las bases de la Hidrostática, en la proposición siete del libro primero de expone claramente el principio que lleva su nombre de la siguiente forma:
Si un cuerpo es más pesado que un fluido y se abandona en éste, se sumergirá hasta el fondo; y si el cuerpo se pesa en el fluido será más ligero que su verdadero peso en un peso igual al peso del líquido desalojado
Numéricamente el problema es sencillo teniendo en cuenta la densidad de los metales y que el peso de un cuerpo es igual al producto del volumen por su peso específico. Supongamos que el lingote de oro pesara un kilogramo.
Si el orfebre hubiera la corona solamente con el lingote de oro, como el peso específico del oro es de 19,32 g/cc, el volumen de la corona sería:
1000 = V · 19,32 ⇒ V = 51,76 cc
Si el orfebre hubiera hecho trampas y hubiera empleado, por ejemplo, 700 g de oro y sustituidos los 300 restantes por plata, cuyo peso específico es de 10,5 g/cc:
El volumen de oro en la corona del orfebre: 700: 19,32 = 36,23 cc
El volumen de la plata en la corona: 300: 10,5 = 28,57 cc
Por lo tanto, la corona del orfebre tenía un volumen total = 64,8 cc
Es decir, la corona del orfebre tramposo tenía mayor volumen que el que debería tener si hubiera sido fabricada con oro puro. La diferencia de volumen era de unos 13 cc, que es aproximadamente el volumen de una cucharada sopera de un líquido, y, aunque no es excesivamente grande, es apreciable.
La ciencia tiene la propiedad de poder englobar los hechos observacionales en el seno de una teoría general que relaciona diferentes hechos. El principio de Arquímedes, tal y como lo cuenta la leyenda, es un hecho observacional, está relacionado con otros dentro de la Hidrostática y más concretamente, gracias a la ecuación fundamental de la hidrostática y al principio de Pascal, con fenómenos como el equilibrio de gases, la prensa hidráulica y fenómenos relacionados con la presión. El principio de Arquímedes es una consecuencia inmediata de la ecuación fundamental de la hidrostática y al principio de Pascal tal y como se esboza a continuación:
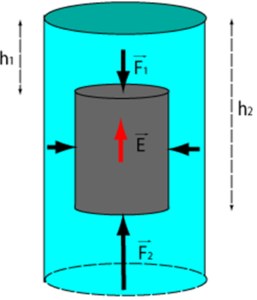
Fig 2: http://slideplayer.es/slide/163138/
La ecuación fundamental de la hidrostática establece que la presión en un punto del interior de un fluido (presión hidrostática) es directamente proporcional a la densidad del fluido y a la la profundidad que se encuentre dicho punto P = d·g·h, donde: P es la presión en un punto del fluido, d es la densidad del fluido, g es la aceleración de la gravedad en el lugar donde se encuentre el fluido y h es la profundidad a que se encuentre el punto respecto a la siperficie del líquido.
El principio de Pascal dice que en un fluido incompresible, en reposo y dentro de un recipiente de paredes indeformables, un cambio de presión aplicado en un punto se transmite íntegramente en todas las direcciones del fluido y actúa perpendicularmente a las paredes que lo contienen.
Si introducimos un cilindro recto de base cubase mide A y de altura H (su volumen será Vcil = A·H).
Sobre cara superior, que se encuentra a una profundidad h1 se ejerce una presión hacia abajo:
P1 = d·g·h1, es decir, que la base superior soporta una fuerza F1 = d·g·h1·A
y sobre cara inferior del cilindro, que se encuentra a una profundidad h2 , se ejerce una presión una presión hacia arriba
P2 = d·g·h2, es decir que la base superior soporta una fuerza F2 = d·g·h2·A
El empuje será la diferencia de las dos fuerzas
E = F2 – F1= d·g·A·(h2 – h1) = d·g·A·H = d·g· Vcil
(se ha tenido en cuenta que la altura del cilindro H = h2 – h1 )
Lo que es el principio de Arquímedes aplicado al cilindro de base A y altura H, que dice que el empuje, E, es igual al peso del volumen del líquido desalojado por el cilindro.