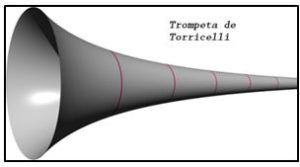
La Trompeta de Torricelli, también conocida como Cuerno o Trompeta de Gabriel es un sólido de revolución que se genera al girar una rama de la hipérbola equilátera alrededor de su asíntota.
La figura fue estudiada en 1641 por E. Torricelli (1608-1647), discípulo de G. Galilei (1564-1642) y también por el matemá boloñés P. Mengoli (1626-1686). Estos científicos italianos descubrieron que la figura tiene una propiedad curiosa y paradójica y es que su volumen es finito, mientras que su superficie lateral es infinita.
Es decir, que es una figura que tiene una capacidad finita, pero no hay pintura en el mundo para cubrir su superficie. Es como si un recipiente se pudiera llenar de pintura roja y no hubiera pintura roja para pintar sus paredes.
Actualmente un estudiante de ciencias de primer año sabe calcular áreas y volúmenes de revolución mediante el Cálculo Integral, es decir, sabe calcular las áreas generadas por una curva plana al girar en torno a una recta situada en su plano y también los volúmenes barridos por una superficie plana al girar alrededor de un eje, situado en su plano.
Si la hipérbola tiene de ecuación: y =1/x
El área de la superficie de revolución generada por la hipérbola al girar alrededor del eje OX es:
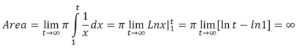
Y el volumen del sólido de revolución engendrado por la superficie plana comprendida entre de la hipérbola y el eje OX al girar alrededor del eje OX es:
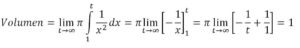
Y es dónde se pone de manifiesto la paradoja: aparece un cuerpo de volumen finito y área lateral infinita
Pero cuando se plantearon el problema ni el gran amigo de Galileo y protector de Torricelli, B. Castelli (1577-1643), ni el propio E. Torricelli, ni P. Mengoli conocían el Cálculo Infinitesimal, que surgiría a finales del siglo XVII de la mano de Newton y Leibniz, y el procedimiento que utilizaron fue el de aproximación por series. Se debe hacer notar que Mengoli, conocía la geometría cartesiana y que, pese a ser discípulo de B. Cavalieri (1598-1647), no utilizó el método de los indivisibles de su maestro.
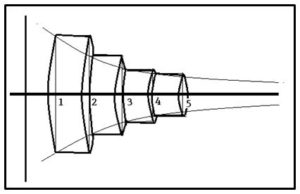
Para poner de manifiesto la paradoja probaron que la superficie de revolución engendrada al girar la hipérbola sería mayor que la suma de las áreas laterales de los cilindros que generaban los rectángulos de base la unidad y altura 1/n al girar en torno a OX y que se muestran en la figura siguiente:
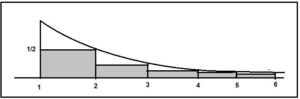
Así el área lateral de la trompeta de Torricelli, Atromp , será mayor que:

Es decir, el área es mayor que la suma de la serie armónica, que fue estudiada por N. de Oresme (1323-1382) hacia 1350 y se sabía que era una serie divergente. El resultado lo obtuvo con una sencilla demostración, acotándola por una suma infinita de números iguales, de esta forma:
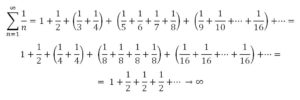
El área de la superficie de revolución era infinita. Sin embargo, el volumen resultó ser finito. Ya que el volumen de la trompeta de Torricelli estaba acotado superiormente por la suma de los volúmenes de los cilindros de altura unidad como se muestran en la figura;
Si acotamos el volumen por cilindros de radio 1/x ( x = 1, 2, 3, …, n, …) y altura 1, se tiene que
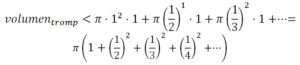
Y se la suma de la serie de los inversos de los cuadrados se sabe que es finita, ya que Mengoli había calculado la suma de la serie telescópica en 1650 y sabía que la serie:
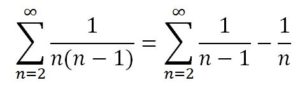
era convergente.
Y con ella se pudo concluir que la suma de los inversos de los cuadrados era convergente, porque se podía acotar superiormente por una serie convergente (la serie telescópica) de la siguiente forma:

Con lo que se probó que el volumen de la trompeta de Torricelli era finito y menor de 2π.




